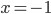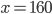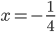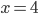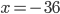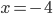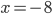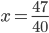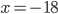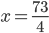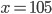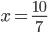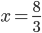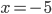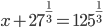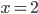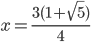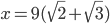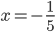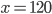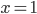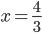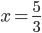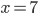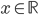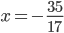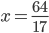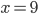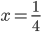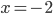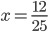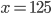Příklad 1

V množině reálných čísel řešte rovnice

(a) 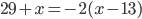$29+x=-2(x-13)$	(b) 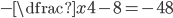$-\dfrac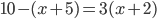{x}{4}-8=-48$	(c) $10-(x+5)=3(x+2)$
(d) 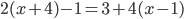$2(x+4)-1=3+4(x-1)$	(e) 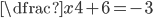$\df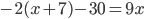rac{x}{4}+6=-3$	(f) $-2(x+7)-30=9x$
(g) 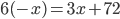$6(-x)=3x+72$	(h) 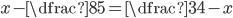$x-\dfrac{8}{5}=\dfrac{3}{4}-x$	(i) 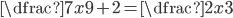$\dfrac{7x}{9}+2=\dfrac{2x}{3}$
(j) 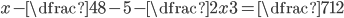$x-\dfrac{4}{8}-5-\dfrac{2x}{3}=\dfrac{7}{12}$	(k) 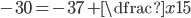$-30=-37+\dfrac{x}{15}$	(l) 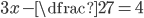$3x-\dfrac{2}{7}=4$
(m) 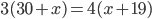$3(30+x)=4(x+19)$	(n) 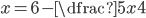$x=6-\dfrac{5x}{4}$	(o) 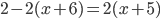$2-2(x+6)=2(x+5)$

Řešení	Ukázat
(a) $x=-1$ , (b) $x=160$ , (c) $x=-\frac14$ , (d) $x=4$ , (e) $x=-36$ , (f) $x=-4$ , (g) $x=-8$ , (h) $x=\frac{47}{40}$ , (i) $x=-18$ , (j) $x=\frac{73}4$ , (k) $x=105$ , (l) $x=\frac{10}7$ , (m) $x=14$ , (n) $x=\frac83$ , (o) $x=-5$

Příklad 2

V množině reálných čísel řešte rovnice

(a) 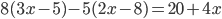$8(3x-5)-5(2x-8)=20+4x$	(b) $x-4[x-2(x+6)]=5x+3$
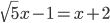
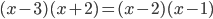
(c) $\sqrt{5}x-1=x+2$	(d) $(x-3)(x+2)=(x-2)(x-1)$
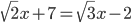
(e) $\sqrt2x+7=\sqrt3x-2$	(f) $x+27^{\frac{1}{3}}=125^{\frac{1}{3}}$

Řešení	Ukázat
(a) $x=2$ , (b) nemá řešení, (c) $x=\frac{3(1+\sqrt5)}4$ , (d) $x=4$ , (e) $x=9(\sqrt2+\sqrt3)$ , (f) $x=2$

Příklad 3

V množině reálných čísel řešte rovnice

(a) 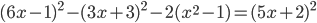$(6x-1)^2-(3x+3)^2-2(x^2-1)=(5x+2)^2$

(b) 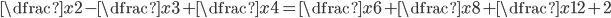$\dfrac{x}{2}-\dfrac{x}{3}+\dfrac{x}{4}=\dfrac{x}{6}+\dfrac{x}{8}+\dfrac{x}{12}+2$

(c) $\dfrac{x}{3}+\dfrac{1}{3}\left\{\dfrac{x}{4}-\dfrac{1}{5}\left[\dfrac{x}{6}+\dfrac{1}{7}\left(\dfrac{x}{8}-1\right)\right]\right\}=\dfrac{x}{3}+\dfrac{x+8}{15}$

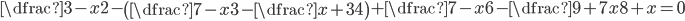
(d) $\dfrac{3-x}{2}-\left(\dfrac{7-x}{3}-\dfrac{x+3}{4}\right)+\dfrac{7-x}{6}-\dfrac{9+7x}{8}+x=0$

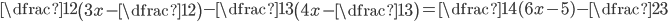
(e) $\dfrac{1}{2}\left(3x-\dfrac{1}{2}\right)-\dfrac{1}{3}\left(4x-\dfrac{1}{3}\right)=\dfrac{1}{4}(6x-5)-\dfrac{2}{3}$

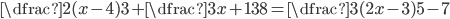
(f) $\dfrac{2(x-4)}{3}+\dfrac{3x+13}{8}=\dfrac{3(2x-3)}{5}-7$

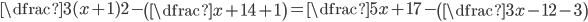
(g) $\dfrac{3(x+1)}{2}-\left(\dfrac{x+1}{4}+1\right)=\dfrac{5x+1}{7}-\left(\dfrac{3x-1}{2}-3\right)$

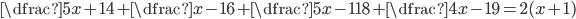
(h) $\dfrac{5x+1}{4}+\dfrac{x-1}{6}+\dfrac{5x-11}{8}+\dfrac{4x-1}{9}=2(x+1)$

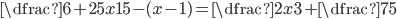
(i) $\dfrac{6+25x}{15}-(x-1)=\dfrac{2x}{3}+\dfrac{7}{5}$

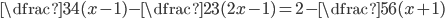
(j) $\dfrac{3}{4}(x-1)-\dfrac{2}{3}(2x-1)=2-\dfrac{5}{6}(x+1)$

Řešení	Ukázat
(a) $x=-\frac15$ , (b) $x=48$ , (c) $x= 120$ , (d) $x=1$ , (e) $x=\frac43$ , (f) $x=49$ , (g) $x=\frac53$ , (h) $x=7$ , (i) $x\in\mathbb R$ , (j) $x=-\frac{35}{17}$

Příklad 4

V množině reálných čísel řešte rovnice

(a) 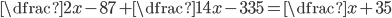$\dfrac{2x-8}{7}+\dfrac{14x-3}{35}=\dfrac{x+3}{5}$	(b) 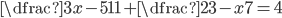$\dfrac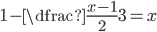{3x-5}{11}+\d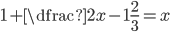frac{23-x}{7}=4$
(c) $1-\dfrac{\frac{x-1}{2}}{3}=x$	(d) $1+\dfrac{2x-1}{\frac{2}{3}}=x$
(e) 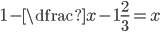$1-\df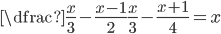rac{x-1}{\frac{2}{3}}=x$	(f) $\dfrac{\frac{x}{3}-\frac{x-1}{2}}{\frac{x}{3}-\frac{x+1}{4}}=x$
(g) 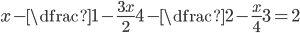$x-\dfrac{1-\frac{3x}{2}}{4}-\dfrac{2-\frac{x}{4}}{3}=2$	(h) 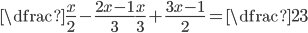$\dfrac{\frac{x}{2}-\frac{2x-1}{3}}{\frac{x}{3}+\frac{3x-1}{2}}=\dfrac{2}{3}$

Řešení	Ukázat
(a) $x=\frac{64}{17}$ , (b) $x= 9$ , (c) $x=1$ , (d) $x=\frac14$ , (e) $x=1$ , (f) $x= -2$ , (g) $x=2$ , (h) $x=\frac{12}{25}$

Příklad 5

V množině reálných čísel řešte rovnici s neznámou 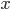$x$ .

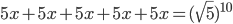
$5x + 5x + 5x + 5x + 5x = (\sqrt5)^{10}$

Řešení	Ukázat
$x=125$

rovnice

Velká kniha rovnic

Lineární rovnice jednoduché

Příklad 1

Příklad 2

Příklad 3

Příklad 4

Příklad 5