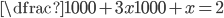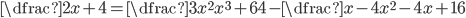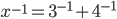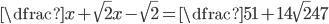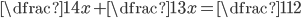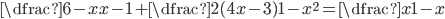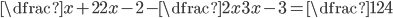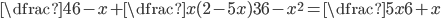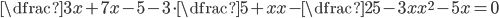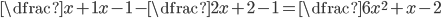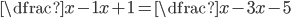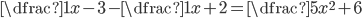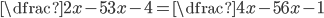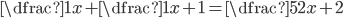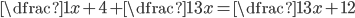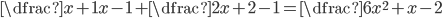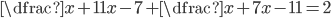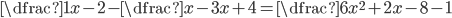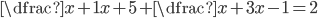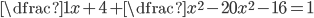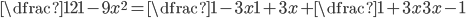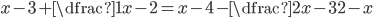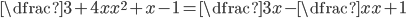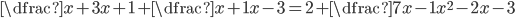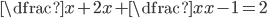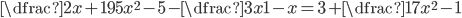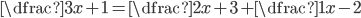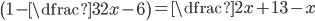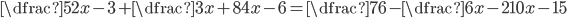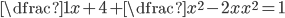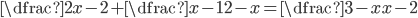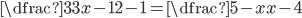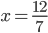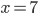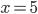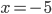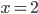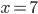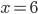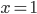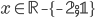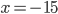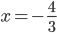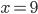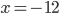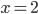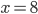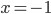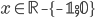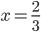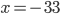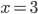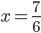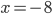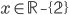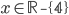Příklad 1
V množině reálných čísel řešte rovnice
(a) 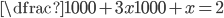
|
(f) 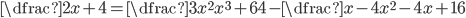
|
(b) 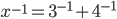
|
(g) 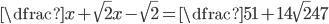
|
(c) 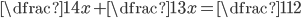
|
(h) 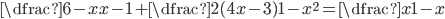
|
(d) 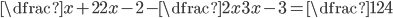
|
(i) 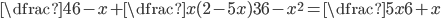
|
(e) 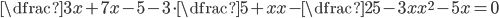
|
(j) 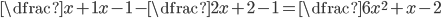
|
| Řešení |
Ukázat |
(a)  , (b) 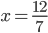 , (c) 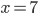 , (d) 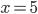 , (e) 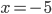 , (f) 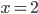 , (g) 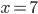 , (h) 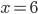 (i) 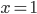 (j) 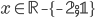
|
Příklad 2
V množině reálných čísel řešte rovnice
(a) 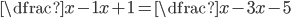
|
(f) 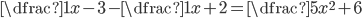
|
(b) 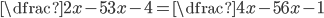
|
(g) 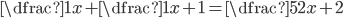
|
(c) 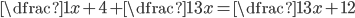
|
(h) 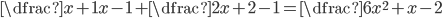
|
(d) 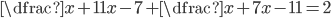
|
(i) 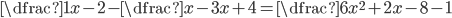
|
(e) 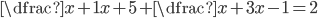
|
(j) 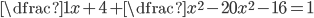
|
| Řešení |
Ukázat |
(a) 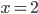 , (b) 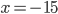 , (c) 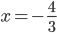 , (d) 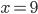 , (e) nemá řešení, (f) 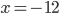 , (g) 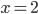 , (h) nemá řešení, (i) nemá řešení, (j) 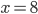
|
Příklad 3
V množině reálných čísel řešte rovnice
(a) 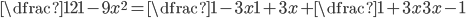
|
(f) 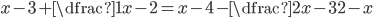
|
(b) 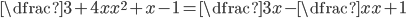
|
(g) 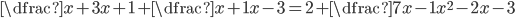
|
(c) 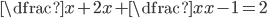
|
(h) 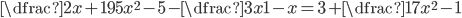
|
(d) 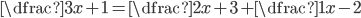
|
(i) 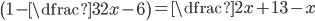
|
(e) 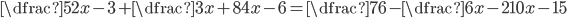
|
(j) 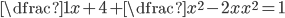
|
| Řešení |
Ukázat |
(a) 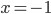 , (b) 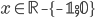 , (c) 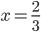 , (d)  , (e) 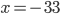 , (f) nemá řešení, (g) nemá řešení, (h) 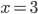 , (i) 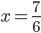 , (j) 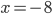
|
Příklad 4
V množině reálných čísel řešte rovnice
(a) 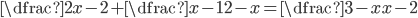
|
(b) 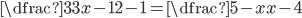
|
|
|
|
|
|
|
|
|
|
|
|
\
|