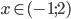Příklad 1
V množině reálných čísel řešte nerovnice
(a) 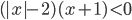
|
(b) 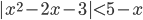
|
(c) 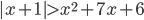
|
(d) 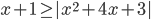
|
(e) 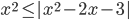
|
(f) 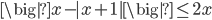
|
(g) 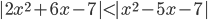
|
(h) 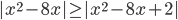
|
(i) 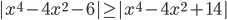
|
(j) 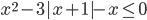
|
(k) 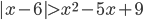
|
(l) 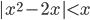
|
(m) 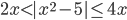
|
(n) 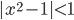
|
(o) 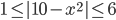
|
(p) 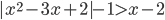
|
(q) 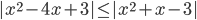
|
(r) 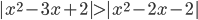
|
| Řešení | Ukázat |
|---|---|
Příklad 2
V množině reálných čísel řešte nerovnice
(a) 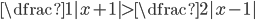
|
(i) 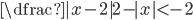
|
(b) 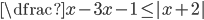
|
(j) 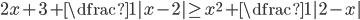
|
(c) 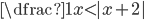
|
(k) 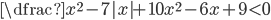
|
(d) 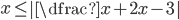
|
(l) 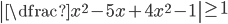
|
(e) 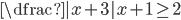
|
(m) 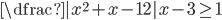
|
(f) 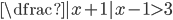
|
(n) 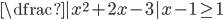
|
(g) 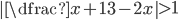
|
(o) 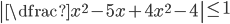
|
(h) 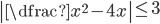
|
(p) 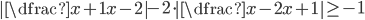
|
| Řešení | Ukázat |
|---|---|
Příklad 3
V množině reálných čísel řešte nerovnice
(a) 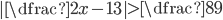
|
(b) 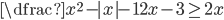
|
(c) 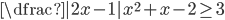
|
(d) 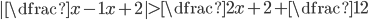
|
(e) 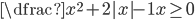
|
(f) 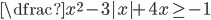
|
(g) 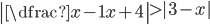
|
(h) 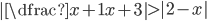
|
(i) 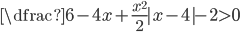
|
(j) 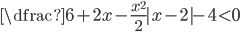
|
(k) 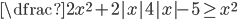
|
(l) 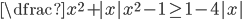
|
(m) 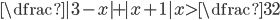
|
(n) 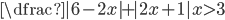
|
(o) 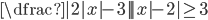
|
| Řešení | Ukázat |
|---|---|
Příklad 4
V množině reálných čísel řešte nerovnice
(a) 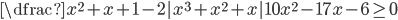
(b) 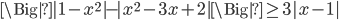
(c) 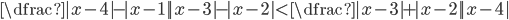
| Řešení | Ukázat |
|---|---|
Příklad 5
Řešte pro 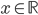 soustavu nerovnic:
soustavu nerovnic:
(a) 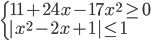
|
(c) 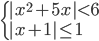
|
(b) 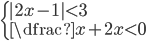
|
(d) 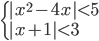
|
| Řešení | Ukázat |
|---|---|
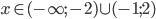
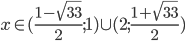
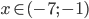
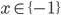
![x\in(-\infty;-\frac32]\cup[\frac{1-\sqrt7}2;\frac{1+\sqrt7}2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ac0318141d1152488b0d985062e83f1f.gif)
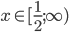
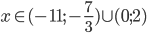
![x\in[4-\sqrt{15};4+\sqrt{15}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3ff8607df4295db12d955ebc273e9018.gif)
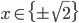
![x\in[2-\sqrt7;2+\sqrt7]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b29fe29f200374660290d87a34e1c847.gif)
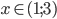
![x\in[1;\sqrt6-1)\cup(\sqrt6+1;5]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a0522106db18828f280e0540eecd2778.gif)
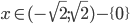
![x\in[-4;-\sqrt{11}]\cup[-3;-2]\cup[2;3]\cup[\sqrt{11};4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ade71a648fef00b5c3ad329685a6b11a.gif)
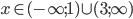
![x\in[0;\frac65]\cup[\frac32;\infty)](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a762529de1a3ebf62ef411d6388dd2a3.gif)
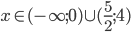
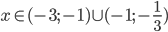
![x\in(-\infty;-1-\sqrt6]\cup(1;\infty)](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d575ed4f74f13aa2f42529620575a76f.gif)
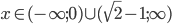
![x\in(-\infty;2+\sqrt6]-\{3\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fb1c2450756923de1074e452ea1e3927.gif)
![x\in(-1;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7088ce6ca0266c24f577806808f2da8e.gif)
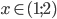
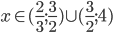
![x\in[-4;-1]\cup[1;4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_63ec36e8d9c0c6d4993f412bfaab8815.gif)
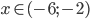
![x\in[-1;3]-\{2\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_9d526d14ec3a0a1ff860bc2cd31cf7a4.gif)
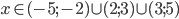
![x\in(-\infty;\frac32]-\{\pm1\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ecae63642edeb9f5d3c836bd643f4a2d.gif)
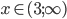
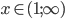
![x\in[0;\frac85]\cup[\frac52;\infty)](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_edde9d186d0a508f0577a3493ca557b6.gif)
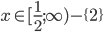
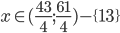
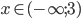
![x\in[\frac{-5-\sqrt{109}}6;-2)\cup(1;\frac{\sqrt{61}-1}6]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6e8b392e5b82f73405fc556c79190090.gif)
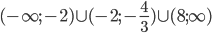
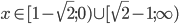
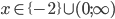
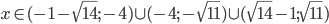
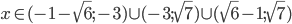
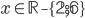
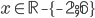
![x\in[-2;-\frac54)\cup\{0\}\cup(\frac54;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6bdca893d78206d3f18730ccf4963bb1.gif)
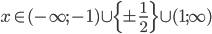
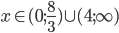
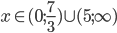
![x\in[-3;-\frac92]\cup[\frac95;3]\setminus\{\pm2\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a20414a26e41c875fb6e9a348828078e.gif)
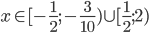
![x\in(-\infty;-1]\cup\{1\}\cup[2;\infty)](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c251f95681bc0c7d01e6d20f4e722636.gif)
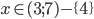
![x\in[0;\frac{12+\sqrt{331}}{17}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e525b88da91b42ded2e2a0ab98ab632a.gif)
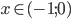
![x\in(-2;0]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_45d3c51fdd1ef59b23e76f3d178c17c3.gif)