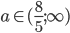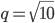Příklad 1
V množine 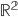 řešte rovnice s neznámými
řešte rovnice s neznámými 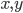 a s parametrem
a s parametrem 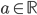 :
:
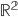 řešte rovnice s neznámými
řešte rovnice s neznámými 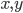 a s parametrem
a s parametrem 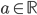 :
:
Určete hodnotu parametru 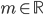 tak, aby řešením soustavy byla dvě kladná čísla.
tak, aby řešením soustavy byla dvě kladná čísla.
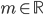 tak, aby řešením soustavy byla dvě kladná čísla.
tak, aby řešením soustavy byla dvě kladná čísla.
Pro které hodnoty parametru 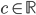 nemá soustava
nemá soustava 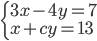 řešení?
řešení?
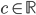 nemá soustava
nemá soustava 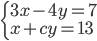 řešení?
řešení?
| Řešení | Ukázat |
|---|---|
Příklad 4
Soustava 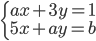 má nekoněčně mnoho řešení. Určete parametry
má nekoněčně mnoho řešení. Určete parametry 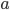 a
a 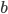 .
.
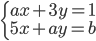 má nekoněčně mnoho řešení. Určete parametry
má nekoněčně mnoho řešení. Určete parametry 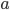 a
a 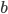 .
.
| Řešení | Ukázat |
|---|---|
Příklad 5
Pro které hodnoty parametru 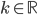 má soustava
má soustava 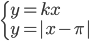 právě dvě reálná řešení?
právě dvě reálná řešení?
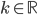 má soustava
má soustava 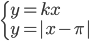 právě dvě reálná řešení?
právě dvě reálná řešení?
| Řešení | Ukázat |
|---|---|
Příklad 6
Určete hodnotu parametru 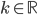 tak, aby soustava rovnic
tak, aby soustava rovnic 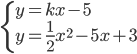 měla právě jedno řešení.
měla právě jedno řešení.
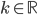 tak, aby soustava rovnic
tak, aby soustava rovnic 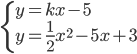 měla právě jedno řešení.
měla právě jedno řešení.
| Řešení | Ukázat |
|---|---|
Příklad 7
Určete hodnotu parametru 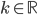 tak, aby pro řešení soustavy
tak, aby pro řešení soustavy 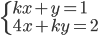 platilo
platilo 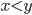 .
.
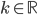 tak, aby pro řešení soustavy
tak, aby pro řešení soustavy 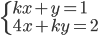 platilo
platilo 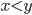 .
.
| Řešení | Ukázat |
|---|---|
Příklad 8
Určete všechny dvojice ![[x;y]\in\mathbb{N}^2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_96acf8d5a52ffaceb9f11a72b642c59d.gif) , pro které platí
, pro které platí 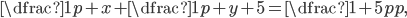 kde
kde 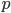 je prvočíslo.
je prvočíslo.
![[x;y]\in\mathbb{N}^2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_96acf8d5a52ffaceb9f11a72b642c59d.gif) , pro které platí
, pro které platí 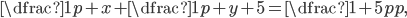 kde
kde 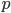 je prvočíslo.
je prvočíslo.
| Řešení | Ukázat |
|---|---|
Příklad 9
Určete všechny hodnoty parametru 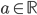 , pro které soustava
, pro které soustava 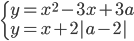 nemá řešení.
nemá řešení.
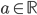 , pro které soustava
, pro které soustava 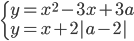 nemá řešení.
nemá řešení.
| Řešení | Ukázat |
|---|---|
Příklad 10
Určete všechny hodnoty parametru 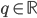 , pro které má soustavy
, pro které má soustavy 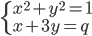 právě jedno řešení, které leží v 1. kvadrantu.
právě jedno řešení, které leží v 1. kvadrantu.
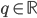 , pro které má soustavy
, pro které má soustavy 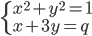 právě jedno řešení, které leží v 1. kvadrantu.
právě jedno řešení, které leží v 1. kvadrantu.
| Řešení | Ukázat |
|---|---|
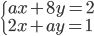
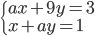
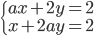
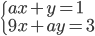
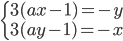
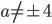
![[x;y]=[\frac2{a+4};\frac1{a+4}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_54c8261c41aaed9031fb7a0af05243d6.gif)
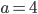
![[x;y]=[t;\frac{1-2t}4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6e34a6edd606c01d5c7fd2dc6aeb3a7e.gif)
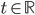
![[x;y]=[\frac3{a+3};\frac1{a+3}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_bfb587522e662554436b1619ecec5fad.gif)
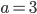
![[x;y]=[t;\frac{1-t}3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d4c4c624f9bcbe14e1f69c50cb462bec.gif)
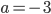
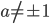
![[x;y]=[\frac2{a+1};\frac1{a+1}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e776c9ed7628da8287556e34666b029a.gif)
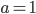
![[x;y]=[t;\frac{2-t}2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_885af88cd592eae58243fe67cd3b2112.gif)
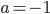
![[x;y]=[\frac1{a+3};\frac3{a+3}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d05961f54f2d00f8d9ca2d5a5bfd390a.gif)
![[x;y]=[t;1-3t]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_945f507074894cb8d17a755dd8de53af.gif)
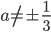
![[x;y]=[\frac3{3a+1};\frac3{3a+1}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1aa064800883f3bf164a64b903ce5e99.gif)
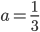
![[x;y]=[t;3-t]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d3320fa71e4cff9154b87c03477893b0.gif)
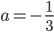
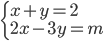
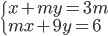
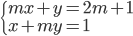
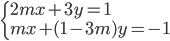
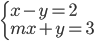
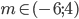
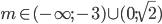
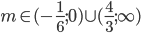
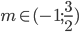
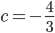
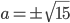
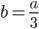
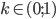
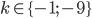
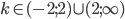
![[x;y]\in\{[1;p^2];[p;p],[p^2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_10fac2a6c87fb97b3317a748dce2c68e.gif)