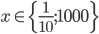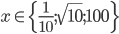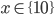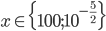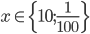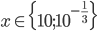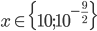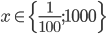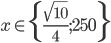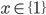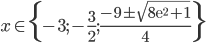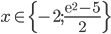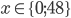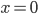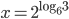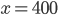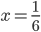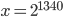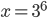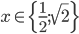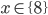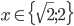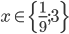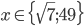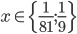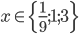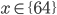Příklad 1
Řešte rovnice pro 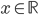 :
:
(a) 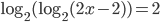
|
(b) 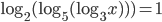
|
(c) 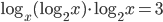
|
(d) 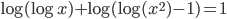
|
(e) ![\log_2\left[\dfrac{\log_3(6x-2)}{\log_3(x-3)}\right]=1](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_edb0876812b7168543091352719d7367.gif)
|
(f) 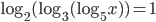
|
| Řešení | Ukázat |
|---|---|
Příklad 2
Řešte rovnice pro 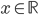 :
:
(a) 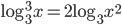
|
(b) 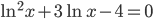
|
(c) 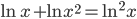
|
(d) 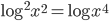
|
(e) 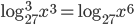
|
(f) 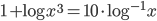
|
(g) 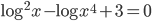
|
(h) 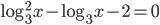
|
(i) 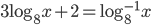
|
(j) 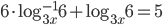
|
| Řešení | Ukázat |
|---|---|
Příklad 3
Řešte rovnice pro 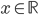 :
:
(a) 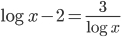
|
(b) 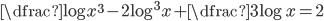
|
(c) 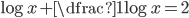
|
(d) 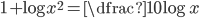
|
(e) 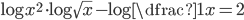
|
(f) 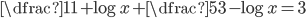
|
(g) 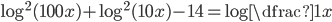
|
(h) 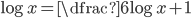
|
(i) 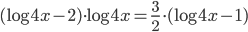
|
(j) ![\sqrt[3]{1+\ln x}+\sqrt[3]{1-\ln x}=2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_925650204f3806d3a66336590366ccf6.gif)
|
| Řešení | Ukázat |
|---|---|
Příklad 4
Řešte rovnice pro 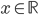 :
:
(a) 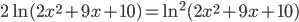
|
(b) 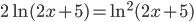
|
| Řešení | Ukázat |
|---|---|
Příklad 5
Řešte rovnice pro 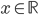 :
:
(a) 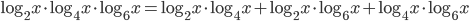
|
(b) 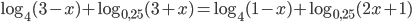
|
| Řešení | Ukázat |
|---|---|
Příklad 6
Řešte rovnice pro 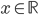 :
:
(a) 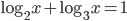
|
(b) 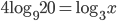
|
(c) 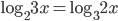
|
(d) 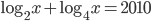
|
(e) 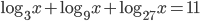
|
(f) 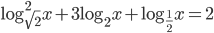
|
| Řešení | Ukázat |
|---|---|
Příklad 7
Řešte rovnice pro 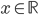 :
:
(a) 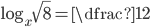
|
(b) 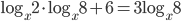
|
(c) 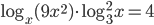
|
(d) 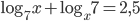
|
(e) 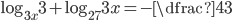
|
(f) 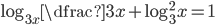
|
(g) 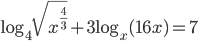
|
(h) 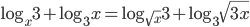
|
| Řešení | Ukázat |
|---|---|
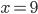
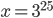
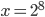
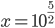
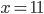
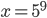
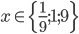
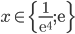
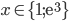
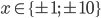
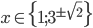
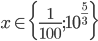
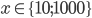
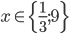
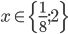
![x=\{\sqrt{\frac23};\sqrt[3]{\frac29}\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_37790c5f034af8e950dd652a1d7ab034.gif)