Příklad 1
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 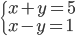
|
(b) 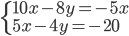
|
(c) 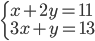
|
(d) 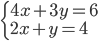
|
(e) 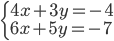
|
(f) 
|
(g) 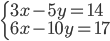
|
(h) 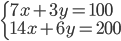
|
(i) 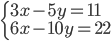
|
(j) 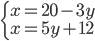
|
(k) 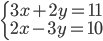
|
(l) 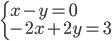
|
(m) 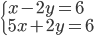
|
(n) 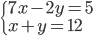
|
(o) 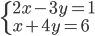
|
(p) 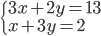
|
(q) 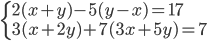
|
(r) 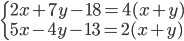
|
(s) 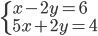
|
(t) 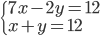
|
| Řešení | Ukázat |
|---|---|
Příklad 2
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 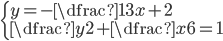
|
(b) 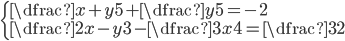
|
(c) 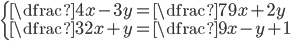
|
(d) 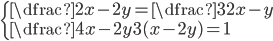
|
(e) 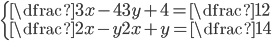
|
(f) 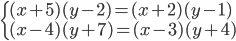
|
(g) 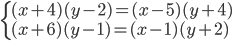
|
(h) 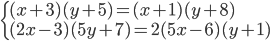
|
| Řešení | Ukázat |
|---|---|
Příklad 3
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 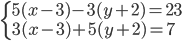
|
(b) 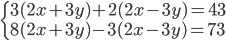
|
(c) 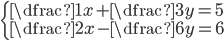
|
(d) 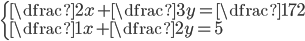
|
(e) 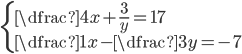
|
(f) 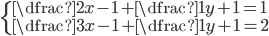
|
(g) 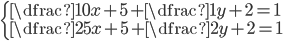
|
(h) 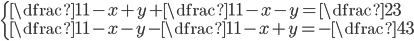
|
(i) 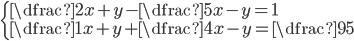
|
(j) 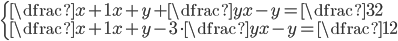
|
(k) 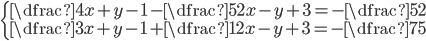
|
(l) 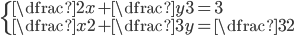
|
| Řešení | Ukázat |
|---|---|
Příklad 4
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 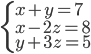
|
(b) 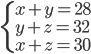
|
(c) 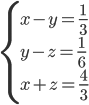
|
(d) 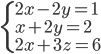
|
(e) 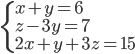
|
(f) 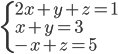
|
(g) 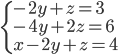
|
(h) 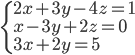
|
| Řešení | Ukázat |
|---|---|
Příklad 5
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 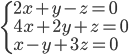
|
(b) 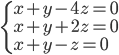
|
(c) 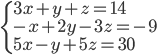
|
(d) 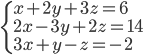
|
(e) 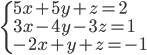
|
(f) 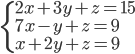
|
(g) 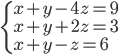
|
(h) 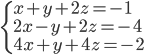
|
(i) 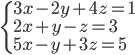
|
(j) 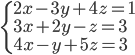
|
(k) 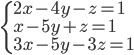
|
(l) 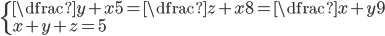
|
(m) 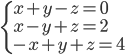
|
(n) 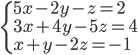
|
| Řešení | Ukázat |
|---|---|
Příklad 6
V  rešte soustavy rovnic:
rešte soustavy rovnic:
(a) 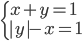
|
(b) 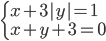
|
(c) 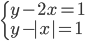
|
(d) 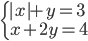
|
(e) 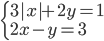
|
(f) 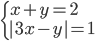
|
(g) 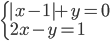
|
(h) 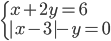
|
(i) 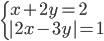
|
(j) 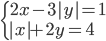
|
(k) 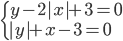
|
(l) 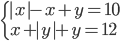
|
(m) 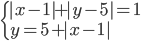
|
(n) 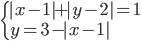
|
(o) 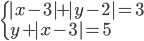
|
(p) 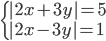
|
(q) 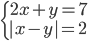
|
(r) 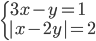
|
| Řešení | Ukázat |
|---|---|
![[x;y]=[3;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b685ae3e3b1177fc8e866f0f206f0a43.gif)
![[x;y]=[8;15]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ade30dbf35da4400eac628d4a7f96eb9.gif)
![[x;y]=[3;4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d58a89a65c5ae2a15f4241eccbaea8df.gif)
![[x;y]=[3;-2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_4f24238dad3b6e24224619871c9b3707.gif)
![[x;y]=[-\frac12;-2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3871abb1c2ebee6d277045b9ff11dede.gif)
![[x;y]=[8;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_899023fa00f81822279acfffd0b6ecce.gif)
![[x;y]=[t;\frac{100-7t}3]\ t\in\mathbb R](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c415206bca899b758f2d0dfd279a2fdd.gif)
![[x;y]=[t;\frac{3t-11}5]\ t\in\mathbb R](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_71072889e47d589540630f17ac55662b.gif)
![[x;y]=[17;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2c2aa3afcb4eddc48df83f645b541dd3.gif)
![[x;y]=[\frac{53}{13};-\frac8{13}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_5b56d25522f7ea2eb54a9962c56d3aaa.gif)
![[x;y]=[2;-2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_daef6429264fa305dd83be67aa763967.gif)
![[x;y]=[\frac{29}9;\frac{79}9]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1592d7efdb4820b588bc0f3178e39f9a.gif)
![[x;y]=[2;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8f474fa857624cc7a0c9238a5c030bc7.gif)
![[x;y]=[5;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1095b7e754c07df9e3c3262cff776a8e.gif)
![[x;y]=[2;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e531e5f78296a93b99db5b692b7b6c1b.gif)
![[x;y]=[-49;-\frac{80}3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0d04d9179beaebd699a0341126023a4c.gif)
![[x;y]=[4;8]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8af62f67d9e49942fcfd7c369f0bbda2.gif)
![[x;y]=[3t;2-t]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f8a8255cff26c666d1417ced938c0f39.gif)
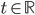
![[x;y]=[-2;-4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_97f0c749c2ff44557f64ac47cb80f95d.gif)
![[x;y]=[1;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dd440388c81b8087b52b4a969cdea038.gif)
![[x;y]=[t;-\frac t4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0028264df27a7e38b8cdb0a7fb69f616.gif)
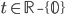
![[x;y]=[5;6]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_9b1a617beb4967656acef8d2388ed85c.gif)
![[x;y]=[7;5]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1312002e610133e51bbd609ea0337533.gif)
![[x;y]=[8;4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f3893162a110401cadc7cb4104c52e9b.gif)
![[x;y]=[3;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_264041055ce2d68c2ba3c0b3fd4d0b81.gif)
![[x;y]=[7;-3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cb3d8af263fa91b5ec9c06e89dc8d872.gif)
![[x;y]=[4;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cc2a973f99c69e418cbd38cbb1b02662.gif)
![[x;y]=[\frac14;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2580b7f4308de4864cd01f34a48abebe.gif)
![[x;y]=[\frac12;\frac23]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1f9cdf5d21602776df6d174852f85d8b.gif)
![[x;y]=[\frac12;\frac13]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6837458d2ed65e3c4a50d85f80307f14.gif)
![[x;y]=[-10;-\frac53]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_51bea28f6859f5cd1684f61ebd1fbf55.gif)
![[x;y]=[2;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6537953e12ae89f78c74ad86659a16be.gif)
![[x;y]=[2;\frac25]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_238714e06de367fc630f814430fbfb6b.gif)
![[x;y]=[2;-3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_82216f93ba1598d6f8e6daf9680471e0.gif)
![[x;y[\in\{[1;3];[2;6]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c6684ccf4f42968befa288acd21d89c3.gif)
![[x;y;z]=[20;-13;6]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b73305c2e7218ea5d42923bdd8c8afd3.gif)
![[x;y;z]=[13;15;17]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b4cd088852a01dac290dd8b94d11b134.gif)
![[x;y;z]=[\frac{11}{12};\frac{7}{12};\frac{5}{12}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_89e47c88e5d4925c8cad5d813512da1d.gif)
![[x;y;z]=[1;\frac12;\frac43]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_76e942b1895cc0961f3826ff0a11a3ff.gif)
![[x;y;z]=[\frac{33}4;-\frac94;\frac14]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_eb750764816c1f817ca2910b6f1ab013.gif)
![[x;y;z]=[-\frac72;\frac{13}2;\frac32]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_72c57e6802af05e88a0ce57a90a7a88e.gif)
![[x;y;z]=[1;t;2t+3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1eadb42dafc3d67903bb3b1e1697dad7.gif)
![[x;y;z]=[1;1;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_4c72b7d44b0f025052328a89b6129678.gif)
![[x;y;z]=[0;0;0]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_bfa4341e667dedecae9cb43fbe759c69.gif)
![[x;y;z]=[t;-t;0]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_60006405938986f839ceb9dd0038219d.gif)
![[x;y;z]=[1;5;6]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f09647f7191e32eaa78c85d6baf443cd.gif)
![[x;y;z]=[1;-2;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7a9792ad7366e1ec7287e15546776b44.gif)
![[x;y;z]=[1;-1;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_66ed413216ac56bfc196a33c53fbf5d9.gif)
![[x;y;z]=[2;4;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ec38e1f5f3ce47362b784ddaf980c54a.gif)
![[x;y;z]=[t,5-t;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a86f085456b28292fb2aa7c68eecd14f.gif)
![[x;y;z]=[1;2;-2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e6d8b053d858fa068c2ef0465c6b4045.gif)
![[x;y;z]=[t;s;2t+s-3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_408bc55e9b5427f9115a60db475cbfc1.gif)
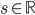
![[x;y;z]=[\frac{27}{31};\frac5{31};-\frac2{31}]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_af9fdff4a22059b67fc6de739c83390a.gif)
![[x;y;z]=[\frac23;0;\frac13]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_28495db587e31c9742023eae08596dca.gif)
![[x;y;z]=[-5;5;5]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_26ed94971e257d307b0add1e621de6b0.gif)
![[x;y;z]=[1;2;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_03873facf62fdd41768903d468cb8221.gif)
![9?x;y;z]=[-1;-2;-3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ad35eeef3d7034abf7e1799c061a1f2d.gif)
![[x;y]=[0;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b3f411c6a911bd635bb7fef0229ae050.gif)
![[x;y]\in\{[-5;2],[-2;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_649c7cdf15155d4d7413b8d7604b0966.gif)
![[x;y]\in\{[-\frac23;\frac73];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_37cbcd0e8333d3aa513489184ad7c698.gif)
![[x;y]\in\{[\frac14;\frac74];[\frac34;\frac54]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_78b05018ac71f212a5e5705f0f4312b9.gif)
![[x;y]\in[0;-1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b20e2ac530db6527528f6f448112a300.gif)
![[x;y]\in\{[0;3];[4;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_074076ce839869be2c78beb5dcea4b95.gif)
![[x;y]\in\{[\frac47;\frac57];[\frac87;\frac37]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6b69a205811b1588d46b903f78ea1a18.gif)
![[x;y]\in\{[-6;9];[0;-3];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a03af7f9e1734eef52571b63c3e08377.gif)
![[x;y]=[-\frac85;\frac{34}5]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3311e590b76669325b69939cf5b06ae2.gif)
![[x;y]\in\{[\frac12;\frac{11}2]; [\frac32;\frac{11}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6dfefeb2e8eac4b7ed2a228733a7b28d.gif)
![[x;y]\in\{[t;3-|t-1|], 0\le t\le2\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_30b55d8de076a1585d93856e11bf614e.gif)
![[x;y]\in\{[t;5-|x-3|], 0\le t\le6\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a367e98f39c9685aea2b1c7d4a56f852.gif)
![[x;y]\in\{[-\frac32;-\frac23];[-1;1];[1;1];[\frac32;\frac23]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_bc5fba0650a0e751c5a8cd7942da4de5.gif)
![[x;y]\in\{[3;1];[\frac53;\frac{11}3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f14eddf500208f066d4301d013bd3a42.gif)
![[x;y]\in\{[0;-1];[\frac45;\frac75]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6a98bac730863f961347d805df5dfff6.gif)