Příklad 1
V množině 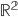 řešte soustavy
řešte soustavy
(a) 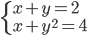
|
(b) 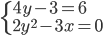
|
(c) 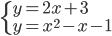
|
(d) 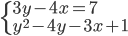
|
(e) 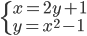
|
(f) 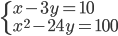
|
| Řešení | Ukázat |
|---|---|
Příklad 2
V množině 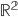 řešte soustavy
řešte soustavy
(a 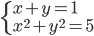
|
(b) 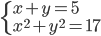
|
(c) 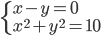
|
(d) 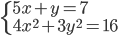
|
(e) 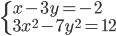
|
(f) 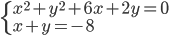
|
(g) 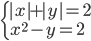
|
(h) 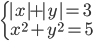
|
(i) 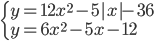
|
(j) 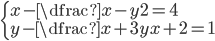
|
| Řešení | Ukázat |
|---|---|
Příklad 3
Rešte pro 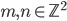 soustavu
soustavu
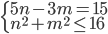
| Řešení | Ukázat |
|---|---|
Příklad 4
V množině 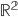 řešte soustavy
řešte soustavy
(a) 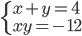
|
(b) 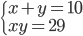
|
(c) 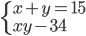
|
(d) 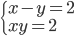
|
(e) 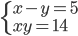
|
(f) 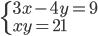
|
(g) 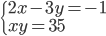
|
(h) 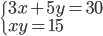
|
| Řešení | Ukázat |
|---|---|
Příklad 5
V množině 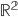 řešte soustavy
řešte soustavy
(a) 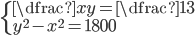
|
(b) 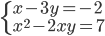
|
(c) 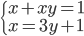
|
(d) 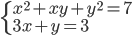
|
(e) 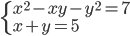
|
(f) 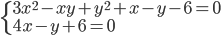
|
(g) 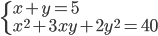
|
(h) 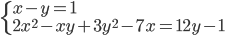
|
(i) 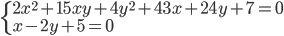
|
(j) 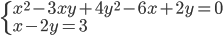
|
(k) 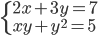
|
(l) 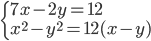
|
(m) 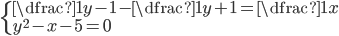
|
(n) 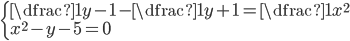
|
| Řešení | Ukázat |
|---|---|
Příklad 6
V množině 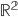 řešte soustavy
řešte soustavy
(a) 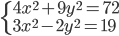
|
(b) 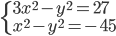
|
(c) 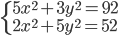
|
(d) 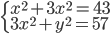
|
(e) 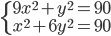
|
(f) 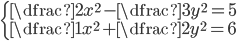
|
(g) 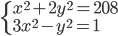
|
(h) 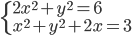
|
(i) 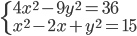
|
(j) 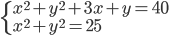
|
(k) 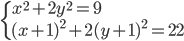
|
(l) 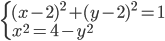
|
(m) 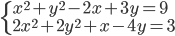
|
(n) 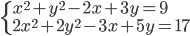
|
| Řešení | Ukázat |
|---|---|
Příklad 7
V množině 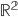 řešte soustavy
řešte soustavy
(a) 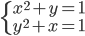
|
(b) 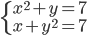
|
(c) 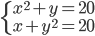
|
(d) 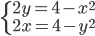
|
(e) 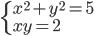
|
(f) 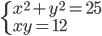
|
(g) 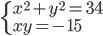
|
(h) 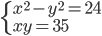
|
| Řešení | Ukázat |
|---|---|
Příklad 8
V množině 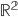 řešte soustavy
řešte soustavy
(a) 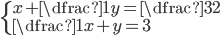
|
(b) 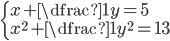
|
(c) 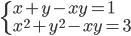
|
(d) 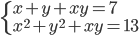
|
(e) 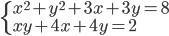
|
(f) 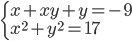
|
(g) 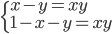
|
(h) 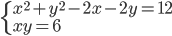
|
(i) 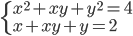
|
(j) 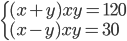
|
(k) 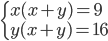 (l) (l)
|
(l) 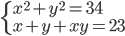
|
(m) 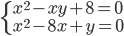
|
(n) 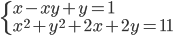
|
(o) 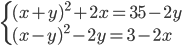
|
(p) 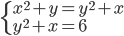
|
| Řešení | Ukázat |
|---|---|
Příklad 9
V množině 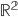 řešte soustavy
řešte soustavy
(a) 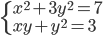
|
(b) 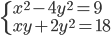
|
(c) 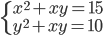
|
(d) 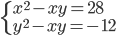
|
(e) 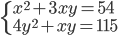
|
(f) 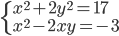
|
(g) 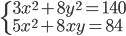
|
(h) 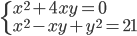
|
(i) 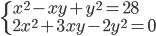
|
(j) 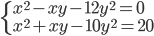
|
(k) 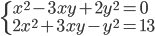
|
(l) 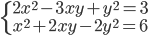
|
(m) 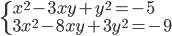
|
(n) 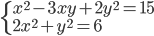
|
(o) 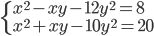
|
(p) 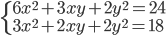
|
| Řešení | Ukázat |
|---|---|
Příklad 10
V množině 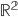 řešte soustavy
řešte soustavy
(a) 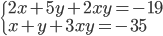
|
(b) 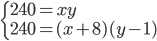
|
(c) 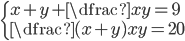
|
(d) 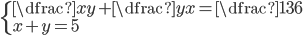
|
(e) 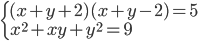
|
(f) 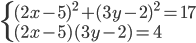
|
(g) 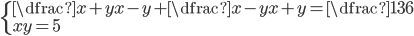
|
(h) 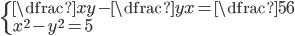
|
(i) 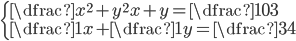
|
(j) 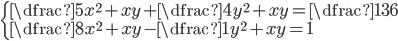
|
(k) 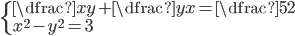
|
(l) 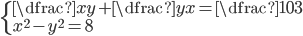
|
(m) 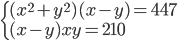
|
(n) 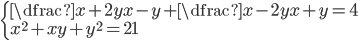
|
(o) 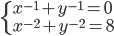
|
(p) 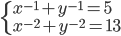
|
(q) 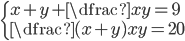
|
(r) 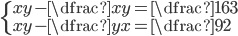
|
| Řešení | Ukázat |
|---|---|
Příklad 11
V množině 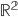 řešte soustavy
řešte soustavy
(a) 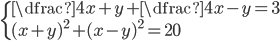
|
(b) 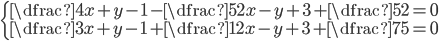
|
(c) 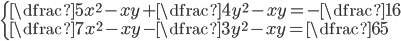
|
(d) 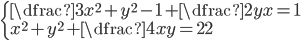
|
(e) 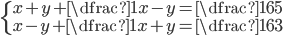
|
(f) 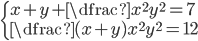
|
| Řešení | Ukázat |
|---|---|
![[x;y]\in\{[0;2];[3;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_4c1aef327059aa79270862d45b1a01cb.gif)
![[x;y]\in\{[6;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_eee59e933162effb2ebae101b33fc66f.gif)
![[x;y]\in\{[-1;1];[4;11]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7b1c4700e9d53da4b8d8c13e19a08642.gif)
![[x;y]\in\{[-\frac{13}{16};\frac54];[2;5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_5bcb363fa9232713029bf9e3d0a36c6d.gif)
![[x;y]\in\{[-\frac12;-\frac34];[1;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a44ec2efd63352140f56601f22c8b5bb.gif)
![[x;y]\in\{[-2;-4];[10;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_27a2beda805124aa0c430fe881118b67.gif)
![[x;y]\in\{[-1;2];[2;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b28fbe5e7f8e59c0c6c2d33b4547e13b.gif)
![[x;y]\in\{[1;4];[4;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f65701301534713d4b7ec9c145f9c221.gif)
![[x;y]=\{[-\sqrt5;-\sqrt5];[\sqrt5;\sqrt5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f448cdcac5755b98caef85420ff73f84.gif)
![[x;y]\in\{[\frac{131}{79};-\frac{102}{79}];[1;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d473057ffc6a905574e665c13f18e81a.gif)
![[x;y]\in\{[-2;0];[\frac{17}5;\frac95]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_46547cdb10d61eebbf64d05e372c85ce.gif)
![[x;y]\in\{[-6;-2];[-4;-4]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_32d3cc193e5a6217031d4e15be0036ca.gif)
![[x;y]\in\{[0;-2];[\pm1;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c15e42ed3ef5e6c834888ee724b49f34.gif)
![[x;y]\in\{[-2;\pm1];[-1;\pm2];[1;\pm2];[2;\pm1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_071102bb191bc58a4a2da8c3dd0e1b4f.gif)
![[x;y]\in\{[2;2];[-3;57]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_5e9ae1f464b5534430f9c9b886bc8d0a.gif)
![[x;y]=\{[2;6];[5;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_77517bb47233fb93ee17ab11959e5ed3.gif)
![[m;n]=[0;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f7607c9e6f22618210e9a5478ed5f256.gif)
![[x;y]\in\{[-2;6];[6;-2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6f9f570299196803e7447a171fe80d25.gif)
![[x;y]\in\emptyset](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e75690d62979b982a7ab15a5a0b4b923.gif)
![[x;y]\in\{[-2;17];[17;-2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c97a1f86b3339fa8dd22d24096cf1d17.gif)
![[x;y]\in\{[1-\sqrt3;-1-\sqrt];[1+\sqrt3;\sqrt3-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cfb587595d6eafb78af003017a66ec69.gif)
![[x;y]\in\{[-2;-7];[7;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_64513e4264b502f45f2252ce8c12a480.gif)
![[x;y]\in\{[7;3];[-4;-\frac{21}4]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fabd1f5354b4a16b538e691fe8aa8107.gif)
![[x;y]\in\{[7;5];[-\frac{15}2;-\frac{14}3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3e33f2a8b72b5829100c50d92fded282.gif)
![[x;y]\in\{[5;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d46f5c451cd48e13ef3132aea0e95970.gif)
![[x;y]\in\{[-15;-45];[15;45]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_45d0366a1d04012d4baa3bddecab55fa.gif)
![[x;y]\in\{[-3;-\frac13];[7;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0965d789ffca10f1c7a03cb1bf32257a.gif)
![[x;y]\in\{[-3;-\frac43];[1;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c19e70eab52429139d6ec11d7fd458be.gif)
![[x;y]\in\{[\frac17;\frac{18}7];[2;-3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0aa72bb0bff3aa8c3e345e7b527337b8.gif)
![[x;y]\in\{[-\frac{5+3\sqrt{17}}2;\frac{15+3\sqrt{17}}2];[\frac{-5+3\sqrt{17}}2;\frac{15-3\sqrt{17}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_792571a8bc40adb2c65acbbb414fdc46.gif)
![[x;y]\in\{[-\frac85;-\frac25];[-1;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dc9165c6db8240990fb061f0fc0dacd7.gif)
![[x;y]\in\{[2;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ba98a51f66f038c79d0eca2c491766ab.gif)
![[x;y]\in\{[-1;2];[-\frac{184}{21};-\frac{79}{42}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_48b55f9ee6662b7a180dd750abbe499e.gif)
![[x;y]\in\{[1;-1];[12;\frac92]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_baf2d20e0dece476cc91dacbb30948c3.gif)
![[x;y]\in\{[3-\sqrt5;2-\sqrt5];[3+\sqrt5;2+\sqrt5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6747eaa010ba3d8e3191de0b06f1348d.gif)
![[x;y]\in\{[-4;5];[\frac12;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dd5a495bf4bf08537251f033080d7b5e.gif)
![[x;y]\in\{[4;8];[\frac{12}5;\frac{12}5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_25717d63d4ee494cf8a2372fb1b2965f.gif)
![[x;y]\in\{[4;-3];[4;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_15795d702f68d6f690ad0f1bc1faf63e.gif)
![[x;y]\in\{[\pm\sqrt{6-2\sqrt3};1-2\sqrt3];[\pm\sqrt{6+2\sqrt3};1+2\sqrt3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c29a1c01762906754be8e0c9bebc8201.gif)
![[x;y]\in\{[-3;\pm2];[3;\pm2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_4cb52ee05b37acedfd51b57c1f1fcda9.gif)
![[x;y]\in\{[-6;\pm9];[6;\pm9]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7d25afc9581efcda258ec95b3e363bca.gif)
![[x;y]\in\{[-4;\pm2];[2;\pm2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_12bfd8e401c637b3320320095f1a985d.gif)
![[x;y]\in\{[-\frac{\sqrt{43}}2;\pm\frac{3\sqrt{11}}2];[\frac{\sqrt{43}}2;\pm\frac{3\sqrt{11}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_730158e1f95254bb97642cb5d6153b6b.gif)
![[x;y]\in\{[-15\sqrt{\frac2{53}};\pm12\sqrt{\frac5{53}}];[15\sqrt{\frac2{53}};\pm12\sqrt{\frac5{53}}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cfc61c6e2a15ce035cbb4381853a2b72.gif)
![[x;y]\in\{[-\frac12;\pm1];[\frac12;\pm1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_29e6b1cc899630a5008f9175f6d51e84.gif)
![[x;y]\in\{[-\sqrt{30};\pm\sqrt{89}];[\sqrt{30};\pm\sqrt{89}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8645dfafc692d063a0c3502ccece6dd6.gif)
![[x;y]\in\{[-1;\pm2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_00cb241b562002482b665ce7306653b0.gif)
![[x;y]\in\{[-3;0];[\frac{57}{13};\pm\frac{16\sqrt3}{13}\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7fbd071d8ce5dcd3d6b562c9c8864b64.gif)
![[x;y]\in\{[4;3];[5;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_de07a486b976beb39f6c4fcc1c9a118e.gif)
![[x;y]\in\{[1;2];[\frac73;\frac43]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1aaf4fc19c27e31a8cb8d41a7ff632b6.gif)
![[x;y]\in\{[\frac{11-\sqrt7}8;\frac{11+\sqrt7}8];[\frac{11+\sqrt7}8;\frac{11-\sqrt7}8]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_95e01a274ebae0353dd613429b88966e.gif)
![[x;y]\in\{[-\frac95;\frac35];[1;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_bfe8edd8ca872e9cdca19dcf4b557325.gif)
![[x;y]\in\{[-\frac52;-\frac32];[1;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ac3cfe6e1f18bfa3d722f83af597c200.gif)
![[x;y]\in\{[\frac{-1-\sqrt5}2;\frac{-1-\sqrt5}2];[\frac{-1+\sqrt5}2;\frac{-1+\sqrt5}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fdf95e7b7e5ce909e824397eeb542474.gif)
![[x;y]\in\{[\frac{-1-\sqrt{29}}2;\frac{-1-\sqrt{29}}2];[\frac{-1+\sqrt{29}}2;\frac{-1+\sqrt{29}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_38d51d33d4a5a2cc89e817ed53bc8728.gif)
![[x;y]\in\{[\frac{1-\sqrt{77}}2;\frac{1+\sqrt{77}}2];[\frac{1+\sqrt{77}}2;\frac{1-\sqrt{77}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7a150352e6f3c7702ffc4083c6f0bd9e.gif)
![[x;y]\in\{[0;2];[2;0];[-1-\sqrt5;-1-\sqrt5];[-1+\sqrt5;-1+\sqrt5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d82e0c73e20e6b3f5021880a0ae4ad91.gif)
![\begin{cases}x^2+y^2=5\\ xy=2\end{cases} \Rightarrow\begin{cases}x^2+y^2=5\\ y=\dfrac2x\end{cases}\Rightarrow\begin{cases}x^2+\dfrac4{x^2}=5\\ y=\dfrac2x\end{cases}\Rightarrow\begin{cases}x^4-5x^2+4=0\\ y=\dfrac2x\end{cases}\Rightarrow\begin{cases}(x^2-4)(x^2-1)=0\\ y=\dfrac2x\end{cases}\\ \Rightarrow \left[\begin{array}{l} [x;y]=[2;1]\\ [x;y]=[-2;-1]\\ [x;y]=[1;2]\\ [x;y]=[-1;-2]\end{array}\right.](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0ebd3187f9eb5eede286fc76d4468f93.gif)
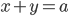
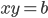
![\begin{cases}x^2+y^2=5\\ xy=2 \end{cases}\Rightarrow\begin{cases}a^2-2b=5\\ b=2\end{cases}\Rightarrow\begin{cases}a^2=9\\b=2 \end{cases}\Rightarrow \left[\begin{array}{l} \begin{cases}x+y=3\\xy=2 \end{cases}\\ \begin{cases}x+y=-3\\ xy=2 \end{cases}\end{array}\right.\Rightarrow \left[\begin{array}{l} [x;y]=[2;1]\\ [x;y]=[1;2]\\ [x;y]=[-2;-1]\\ [x;y]=[-1;-2]\end{array}\right.](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d38debd035575ca63a059e1a4cf4a3a7.gif)
![[x;y]\in\{[-4;-3];[-3;-4];[3;4];[4;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2c885b2b55190df93e77daf10ad1fdcf.gif)
![[x;y]\in\{[-5;3];[-3;5];[3;-5];[5;-3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dd00f685a35b9e84410f4d6f232f3979.gif)
![\begin{cases}x^2-y^2=24&|\cdot35\\-\\xy=35&|\cdot24\end{cases}\Rightarrow\begin{cases}35x^2-24xy-35y^2=0\\xy=35\end{cases}\Rightarrow\begin{cases}(7x+5y)(5x-7y)=0\\xy=35\end{cases}\Rightarrow\\ \Rightarrow\left[\begin{array}{l}\begin{cases}y=-\frac75x\\ xy=35\end{cases}\\ \begin{cases}y=\frac57x\\ xy=35\end{cases}\end{array}\right.\Rightarrow\left[\begin{array}{l}[x;y]=[7;5]\\ [x;y]=[-7;-5]\end{array}\right.](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c60c3fc6f1da15d148b6c0d85ae9a59a.gif)
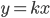
![[0;0]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d8fc3ff72d9f30212c41cc639a7654a8.gif)
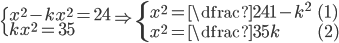
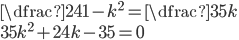
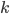
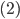
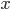
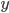
![[x;y]\in\{[\frac12;1];[1;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c7883df61e1bda8a29d91b4af36e3806.gif)
![[x;y]\in\{[2;\frac13];[3;\frac12\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_5788e7be729b072726e24a660078275f.gif)
![[x;y]\in\{[-1;1],[1;-1];[1;2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fac86f31649ea2ed1ed28f9ca508e7e6.gif)
![[x;y]\in\{[1;3];[3;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_aa98db9a20e9142efd43fd280af213ab.gif)
![[x;y]\in\{[-\frac{1+\sqrt{33}}2;\frac{\sqrt{33}-1}2];[\frac{\sqrt{33}-1}2;-\frac{1+\sqrt{33}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_22a47a75fa0a537c92f48343e1642ab7.gif)
![[x;y]\in\{[\frac12;\frac13]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_445f0c56722e3b1dd20c40284bd544cb.gif)
![[x;y]\in\{[3-\sqrt3;3+\sqrt3];[3+\sqrt3;3-\sqrt3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7642adeb053fc98f6346768139b20f3c.gif)
![[x;y]\in\{[0;2];[2;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6520bd247d3fcd6bb09d0115aec2d6b3.gif)
![[x;y]\in\{[-\frac95;-\frac{16}5];[\frac95;\frac{16}5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_4842073c794497127bee6b589a6f0a6b.gif)
![[x;y]\in\{[3;5];[5;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_aaa5d11824d4fc2ca333b9872c077b0d.gif)
![[x;y]\in\{[-1;-9];[4\pm2\sqrt2;8]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_12b27d397ce34a4003aeb928ad873905.gif)
![[x;y]\in\{[-4;1];[1;-4];[1;2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cf4a6df9365e5f7868b905ff8939a992.gif)
![[x;y]\in\{[-5;-2];[-3;-4];[1;4];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_94a1df01036076c74f2f4a81bab0b6f7.gif)
![[x;y]\in\{[-3;-3];[2;2];[\frac{1-\sqrt{21}}2;\frac{1+\sqrt{21}}2];[\frac{1+\sqrt{21}}2;\frac{1-\sqrt{21}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_49f92b6bc886d9a96210eed4905a4c77.gif)
![[x;y]\in\{[-2;-1];[-\frac12;-\frac32];[\frac12;\frac32];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0e52d6ad12f028540de0933dca19248a.gif)
![[x;y]\in\{[-5;-2];[5;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ac4f4cd612a90dbd58aa28f8739e3d78.gif)
![[x;y]\in\{[-3;-2];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8d2fa4f462cda0d6aafd5a6eed77e706.gif)
![[x;y]\in\{[-7;-3];[7;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8f80ce05149c472d97001570ad58be04.gif)
![[x;y]\in\{[-36;\frac{23}2];[-3;-5];[2;5];[36;-\frac{23}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b26996b4363296e0fe196c14e5f400c7.gif)
![[x;y]\in\{[-3;-2];[3;2];[-\frac{\sqrt3}3;-\frac{5\sqrt3}3][\frac{\sqrt3}3;\frac{5\sqrt3}3];\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d4dc6da00b82ed7c522beb59aea89f8f.gif)
![[x;y]\in\{[-6;2];[-2;-4];[2;4];[6;-2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6fee4f3c1fc46b53702b49d0618f4bef.gif)
![[x;y]\in\{[-4;1];[0;\pm\sqrt{21}];[4;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8b156de5abf4dc2d30f9183b07c31cc7.gif)
![[x;y]\in\{[-4;2];[4;-2];[-2\sqrt{\frac73};-4\sqrt{\frac73}];[2\sqrt{\frac73};4\sqrt{\frac73}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_5f9ff114d027905d30b90ecd5e7efed1.gif)
![[x;y]\in\{[-4\sqrt2;-\sqrt2];[4\sqrt2;\sqrt2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ddd25069c2a7a4bf0d8fc137552a7759.gif)
![[x;y]\in\{[-2;-1];[2;1];[-\frac{\sqrt{13}}2;-\frac{\sqrt{13}}2];[\frac{\sqrt{13}}2;\frac{\sqrt{13}}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_71cbd9dea77b1dbdd252fc4f02dcba45.gif)
![[x;y]\in\{[-2;-1];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b31cc5555aa4a799ed3b7c7db70c4a9d.gif)
![[x;y]\in\{[-3;-2];[-2;-3];[2;3];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_918f218ae2d73c5031f6d6d4b0cd543f.gif)
![[x;y]\in\{[-1;2];[1;-2];[-\frac1{\sqrt3};\frac4{\sqrt3}];[\frac1{\sqrt3};-\frac4{\sqrt3}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0f590487f661f557df03405afd23a3c9.gif)
![[x;y]\in\{[-5;-1];[5;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ffa487adebf4d8a0c673b5419e712f37.gif)
![[x;y]\in\{[-2;3];[2;-3];[-\sqrt{\frac65};-2\sqrt{\frac65}];[\sqrt{\frac65};2\sqrt{\frac65}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dea6e4c6d9bd36819d25c9921fcd37e5.gif)
![[x;y]\in\{[2\pm\sqrt{43};\frac{5\mp4\sqrt{43}}{13}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_946dc1e1f5188904512b444831a1d4ba.gif)
![[x;y]\in\{[-48;-5];[40;6]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_330bd7a2a809f175b58751e6ad7b12e8.gif)
![[x;y]\in\{[\frac{10}3;\frac23];[4;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_c9697c75c538324694626561d4078410.gif)
![[x;y]\in\{[2;3];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fb84be51535e320568e2c2b0fe4fad0f.gif)
![[x;y]\in\{[\pm3;0];[0;\pm3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3b832855373de58ec70081da461c35b7.gif)
![[x;y]\in\{[\frac12;\frac13];[2;-\frac23];[3;2];[\frac92;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0d495906830a447e0d4cfe13dd322be1.gif)
![[x;y]\in\{[2;4];[4;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f3b3beb9b1365edb2c1785795984c7c4.gif)
![[x;y]\in\{[3;1];[-3;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_9f7f5240efa6ceeeef86a43f65b60b97.gif)
![[x;y]\in\{[-7;-10];[10;7]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0770669a0b06206053dc299b1ed66ba9.gif)
![[x;y]\in\{[-2\sqrt3;-\sqrt3];[2\sqrt3;\sqrt3];[-2\sqrt7;\sqrt7];[2\sqrt7;\sqrt7]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dd600ecbe9901ff3c6d9f9cb53f9c5bb.gif)
![[x;y]\in\{[-\frac12;\frac12];[\frac12;-\frac12]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f40ada3f7b30b88481d1225d62134bd3.gif)
![[x;y]\in\{[\frac12;\frac3];[\frac13;\frac12]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_40e51f24361d91d486ed2e9ff50e7f89.gif)
![[x;y]\in\{[-2;-3];[2;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2fe0f56f3d1b1b521ef81025329cc3d1.gif)
![x\in\{[3;\pm1];[-\frac53;\pm\frac{\sqrt{65}}3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_640b8ce032355a41565b690bfde74a96.gif)
![x\in\{[2;-3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_77c248c7d999e324e106df3c3a7daf97.gif)
![x\in\{[-5;-3];[5;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_dfc77d3c49cea224cba336f1fd3ac7f6.gif)
![x\in\{[-3;-1];[3;1];[-14\sqrt{\frac2{53}};-4\sqrt{\frac2{53}}];[14\sqrt{\frac2{53}};4\sqrt{\frac2{53}}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_49d6d2294ca19d68be2e76d1242bef04.gif)
![x\in\{[4;1];[\frac4{15};-\frac1{15}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1ea67a0a6c1763a732db34d0ac7f64d3.gif)
![x\in\{[2;1];[6;-3];[6-2\sqrt3;2\sqrt3-2];[6+2\sqrt3;-2-2\sqrt3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_317ed06fe8e53b8acc957f3f854de4dc.gif)