Příklad 1

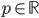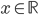Řešte rovnice s parametrem $p\in\mathbb R$ a proměnnou $x\in\mathbb R$ .

(a) $x^2+4x-3p^2+7p-2=0$	(b) $p^2x^2+2p^2x-1+p^2=0$	(c) $(\sqrt{p}-1)x^2+2x\sqrt{p+1}+\sqrt{p}+1=0$
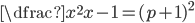
(d) $\dfrac{x^2}{x-1}=(p+1)^2$	(e) $\dfrac{x^2}{2x-1}= p$	(f) $\dfrac{1}{p-x}=\dfrac{1}{p}-\dfrac{1}{x}$
(g) $p(x^2+1)-3=x(x-2p)$	(h) $px(x+3)=x^2+1$	(i) $p^2x=p(x+2)-2$
(j) $x(x-p)=1-p$

Řešení	Ukázat
(a) $x=-2\pm\sqrt{3p^2-7p+6}$ (b) Pro $p\ne0$ je $x=-1\pm\frac1p$ , pro $p=0$ rovnice nemá řešení. (c) Pro $p=1$ je $x=-\frac{\sqrt2}2$ , pro $p\ne1$ je $x=\frac{-\sqrt{p+1}\pm\sqrt2}{\sqrt p-1}$ (d) $p\in(-\infty;-3)\cup(1;\infty)$ : $x=\frac{(p+1)^2\pm(p+1)\sqrt{p^2+2p-3}}2$ , $p\in\{-3;1\}$ : $x=\frac{(p+1)^2}2$ , $p\in(-3;1)$ nemá rovnice řešení. (e) $p\in(-\infty;0)\cup(1;\infty)$ : $x=p\pm\sqrt{p^2-p}$ , $p\in\{0;1\}$ : $x=p$ , $p\in(0;1)$ rovnice nemá řešení. (f) rovnice nemá řešení (g) $p\in(-\infty;\frac34)$ : rovnice nemá řešení, $p=\frac34$ : $x=3$ , $p\in(\frac34;1)\cup(1;\infty)$ : $x=\frac{-p\pm\sqrt{4p-3}}{p-1}$ , $p=1$ : $x=1$ (h) $p\in(-\infty;\frac29(-1-\sqrt{10}))\cup(\frac29(-1+\sqrt{10});1)\cup(1;\infty)$ : $x=\frac{-3p\pm\sqrt{9p^2+4p-4}}{2(p-1)}$ , $p=1$ : $x=\frac13$ , $x\in\{\frac29(-1\pm\sqrt{10})\}$ : $x=\frac{3p}{2(1-p)}$ , $p\in(\frac29(-1-\sqrt{10});\frac29(-1+\sqrt{10}))$ : rovnice nená řešení. (i) $p<\frac78$ : rovnice nemá řešení, $p=\frac78$ : $x=\frac47$ , $x>\frac78$ : $x=\frac{1\pm\sqrt{8p-7}}{2p}$ (j) $p=2$ : $x=1$ , $p\ne2$ : $x\in\{1;p-1\}$

Řešení

Ukázat

(a)

$x=-2\pm\sqrt{3p^2-7p+6}$ (b) Pro

$p\ne0$ je

$x=-1\pm\frac1p$ , pro

$p=0$ rovnice nemá řešení. (c) Pro

$p=1$ je

$x=-\frac{\sqrt2}2$ , pro

$p\ne1$ je

$x=\frac{-\sqrt{p+1}\pm\sqrt2}{\sqrt p-1}$ (d)

$p\in(-\infty;-3)\cup(1;\infty)$ :

$x=\frac{(p+1)^2\pm(p+1)\sqrt{p^2+2p-3}}2$ ,

$p\in\{-3;1\}$ :

$x=\frac{(p+1)^2}2$ ,

$p\in(-3;1)$ nemá rovnice řešení. (e)

$p\in(-\infty;0)\cup(1;\infty)$ :

$x=p\pm\sqrt{p^2-p}$ ,

$p\in\{0;1\}$ :

$x=p$ ,

$p\in(0;1)$ rovnice nemá řešení. (f) rovnice nemá řešení (g)

$p\in(-\infty;\frac34)$ : rovnice nemá řešení,

$p=\frac34$ :

$x=3$ ,

$p\in(\frac34;1)\cup(1;\infty)$ :

$x=\frac{-p\pm\sqrt{4p-3}}{p-1}$ ,

$p=1$ :

$x=1$
(h)

$p\in(-\infty;\frac29(-1-\sqrt{10}))\cup(\frac29(-1+\sqrt{10});1)\cup(1;\infty)$ :

$x=\frac{-3p\pm\sqrt{9p^2+4p-4}}{2(p-1)}$ ,

$p=1$ :

$x=\frac13$ ,

$x\in\{\frac29(-1\pm\sqrt{10})\}$ :

$x=\frac{3p}{2(1-p)}$ ,

$p\in(\frac29(-1-\sqrt{10});\frac29(-1+\sqrt{10}))$ : rovnice nená řešení.
(i)

$p<\frac78$ : rovnice nemá řešení,

$p=\frac78$ :

$x=\frac47$ ,

$x>\frac78$ :

$x=\frac{1\pm\sqrt{8p-7}}{2p}$ (j)

$p=2$ :

$x=1$ ,

$p\ne2$ :

$x\in\{1;p-1\}$

Příklad 2

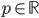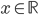Řešte rovnice s parametrem $p\in\mathbb R$ a proměnnou $x\in\mathbb R$ .

(a)

$\sqrt{p-6x}=x-1$

(b)

$\sqrt{p-5x}=1-x$

(c)

$\sqrt{x^2-4p^2}=2p-x$

Řešení	Ukázat
(a) $p<6$ : nemá řešení, $p\ge 6$ : $x=\sqrt{p+3}-2$ (b) $p=-\frac54$ : $x=-\frac32$ , $p\in(-\frac54;5]$ : $x=-\frac32\pm\sqrt{p+\frac54}$ , $p>5$ : $x=-\frac32-\sqrt{p+\frac54}$ (c) $p=0$ : řešení je každé $x\in(-\infty;0]$ , $p\ne0$ : $x=2p$

Příklad 3

(a) Rovnice $x^2+2x-c=0$ má jeden kořen $x_1=1$ . Určete parametr $c$ .
(b) Kvadratická rovnice $x^2-3x+c=0$ má jeden kořen $x_1=3$ . Určete druhý kořen.
(c) Jeden kořen rovnice $x^2-m^2x-m+1=0$ je $x_1=1$ . Určete druhý kořen této rovnice.
(d) Určete parametr $s\in\mathbb{R}$ v rovnici $x^2+10x+s=0$ , když víte, že $x_1=7$ . Určete také $x_2$ .
(e) Určete všechny hodnoty parametru $k\in\mathbb R$ , pro které má rovnice $kx^2+(3k-2)x+k-2=0$ řešení $x_1=0$ . Určete také $x_2$ .
(f) Rovnice $2x^2 + (a-4)x-2a = 0$ s parametem $a\in\mathbb R$ má jeden kořen $x =-3$ . Určete hodnotu parametru a druhý kořen.
(g) Pro které hodnoty parametru $m$ má rovnice $4x^2 - 12x + 9m^2 - 12m + 4 = 0$ s (neznámou $x$ ) nulový kořen?
(h) Rovnice $ax^2 + 5x = 3$ má jedno řešení $x_1 = 1$ . Určete druhý kořen.
(i) Kvadratická rovnice $x^2+9x+m^2+3m+2=0$ má jeden kořen nulový pro dvě hodnoty parametru $m$ . Určete součet těchto hodnot.

Řešení	Ukázat
(a) Dosazením $x_1$ do rovnice dostaneme $c=3$ . (b) $c=0$ (c) $x_2=3$ nebo $x_2=0$ (d) $s=-119$ , $x_2=-17$ (e) $k=2$ , $x_2=-2$ (f) $a=6$ $x_2=2$ (g) $m=\frac23$ (h) $x_2=\frac32$ (i) $m_1+m_2=-3$

Příklad 4

(a) Rovnice $x^2+6x+k=0$ má jeden dvojnásobný kořen. Určete hodnotu $k$ .
(b) Určete, pro jakou hodnotu parametru $k\in\mathbb{R}$ má rovnice $(2-x)(x+1)=k$ v množině reálných čísel jeden dvojnásobný kořen?
(c) Určete všechny hodnoty parametru $k\in\mathbb R$ tak, aby rovnice $x^2+kx+k=0$ měla právě jedno řešení.
(d) Určete parametr $k\in\mathbb R$ tak, aby rovnice $x^2 + 2kx-1 = 2k$ měla právě jeden kořen.
(e) Určete všechny hodnoty parametru $k\in\mathbb R$ tak, aby rovnice $kx^2+2kx+1=0$ měla právě jedno řešení.
(f) Určete všechny hodnoty parametru $k\in\mathbb R$ tak, aby rovnice $kx^2+4kx+4=0$ měla právě jedno řešení.
(g) Pro které hodnoty parametru 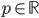$p\in\mathbb R$ má rovnice $x^2+5x+7=px+3$ právě jeden kořen?
(h) Určete všechny hodnoty parametru $a\in\mathbb R$ , pro které má rovnice

$(1-a^2)x^2+2(1+a)x=2$

právě jedno reálné řešení.
(i) Rovnice

$ax^2-2\sqrt{2}x + 1 = 0$ má právě jedno reálné řešení. Určete toto řešení.

Řešení	Ukázat
(a) Diskriminant rovnice musí být roven nule. $k=9$ (b) $k=\frac94$ (c) $k=0$ nebo $k=4$ (d) $k=-1$ (e) $k=1$ (f) $k=1$ (g) $p=1$ nebo $p=9$ (h) $a=1$ nebo $a=3$ (i) $a=0$ $x=\frac{\sqrt2}4$ nebo $a=2$ $x=\frac{\sqrt2}2$

Příklad 5

(a) Pro které hodnoty parametru $c\in\mathbb R$ má rovnice $3x^2-2x+c=0$ dva různé reálné kořeny?
(b) Pro které hodnoty parametru $m\in\mathbb{R}$ má rovnice $(m+5)x^2+4x-m=0$ dva různé reálné kořeny?
(c) Pro které hodnoty parametru $a\in\mathbb{R}$ má rovnice $x^2+(1-a)x+4-a=0$ s neznámou $x$ dva různé reálné nenulové kořeny?
(d) Určete všechna $p\in\mathbb Z$ , pro která má rovnice $px^2+2px+3p-4x-4=0$ dvě různá reálná řešení.
(e) Určete všechny hodnoty parametru $k\in\mathbb R$ , pro které má rovnice $x^2+2(2k-1)x-3k+1=0$ dvě různá reálná řešení.

Řešení	Ukázat
Nápověda: diskriminant rovnice musí být větší než nula. (a) $c\in(-\infty;\frac13)$ (b) $m\in(-\infty;-5)\cup(-1;\infty)$ (c) $a\in(-\infty;-5)\cup(-3;4)\cup(4;\infty)$ (d) $p\in\{\pm1\}$ (e) $k\in(-\infty;0)\cup(\frac14;\infty)$

Příklad 6

(a) Pro které hodnoty parametru $a\in\mathbb{R}$ nemá rovnice $3x^2 + a^2 + a + 1=0$ žádný reálný kořen?
(b) Určete hodnotu parametru $c\in\mathbb{R}$ tak, aby rovnice $3x^2+12x+c=0$ neměla žádné reálné řešení.
(c) Pro které hodnoty parametru $b\in\mathbb R$ nemá rovnice $2x^2+bx+2=0$ žádné reálné řešení?
(d) Pro které hodnoty parametru $k\in\mathbb R$ nemá rovnice $kx^2+5\sqrt2x-3=0$ žádné reálné řešení?

Řešení	Ukázat
Nápověda: Diskriminant rovnice musí být záporný. (a) každé $a\in\mathbb R$ (b) $c>12$ (c) $b\in(-4;4)$ (d) $k\in(-\infty;-\frac{25}6)$

Příklad 7

(a) Pro které hodnoty parametru $p\in\mathbb{R}$ má rovnice $x^2+px+p+3=0$ dvě navzájem různá kladná řešení?
(b) Pro které hodnoty parametru $\lambda\in\mathbb R$ jsou oba (různé) kořeny rovnice $(\lambda-1)x^2+(\lambda-3)x+(\lambda-2)=0$ kladné?
(c) Určete parametr rovnice $x^2+2(p-x)x+p^2+6p=0$ tak, aby rovnice měla dvě navzájem různá kladná řešení?
(d) Určete parametr $t\in\mathbb{R}$ tak, aby rovnice $16x^2 +8(4t-1)x -8t +5=0$ měla dva kořeny stejných znamének.
(e) Pro které hodnoty parametru 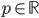$p\in\mathbb R$ mají kořeny rovnice $x^2-2(p-3)x+10-6p=0$ stejná znaménka?
(f) Je dána rovnice $x(x-3) + m(1-x) - 13 = 0$ . Určete všechny hodnoty parametru $m\in\mathbb{R}$ tak, aby kořeny dané rovnice byla dvě navzájem opačná čísla.
(g) Pro které hodnoty parametru 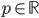$p\in\mathbb R$ jsou kořeny rovnice $5x^2-4(p+3)x+4=p^2$ opačná čísla? Určete tyto kořeny.
(h) Pro které hodnoty parametru $a\in\mathbb R$ je jeden kořen rovnice $(a+5)x^2+x+a-3=0$ kladný a druhý kořen záporný?

Řešení	Ukázat
(a) Nápověda: musí platit $x_1x_2>0$ , $x_1+x_2>0$ a $D>0$ tj. podle Vietových vztahů $\begin{cases}p+3>0\\-p>0\\p^2-4(p+3)>0\end{cases}$ $p\in(-3;-2)$ (b) $\lambda\in(2;1+\sqrt2)$ (c) $p\in(-3-3\sqrt2;-6)$ (d) $t\in(-\infty;-\frac12)\cup(\frac12;\frac58)$ (e) $p\in(-\infty;-1)\cup(1;\frac53)$ (f) $m=-3$ (g) $p=-3$ $x_{1,2}=\pm1$ (h) $a\in(\frac{-2-\sqrt{65}}2;-5)\cup(-5;3)$

Příklad 8

(a) Pro které hodnoty parametru 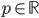$p\in\mathbb R$ je jeden kořen rovnice $x^2-px+(2p+8)=0$ dvakrát větší než druhý?
(b) Pro které hodnoty parametru $a\in\mathbb R$ je jeden kořen rovnice $x^2-(2a+1)x+a^2+2=0$ dvakrát větší než druhý?
(c) Pro které hodnoty parametru $k\in\mathbb R$ je jeden kořen rovnice $4x^2-(2-4k)x+(k^2+1)=0$ dvakrát větší než druhý?
(d) Určete hodnotu parametru $p\in\mathbb{R}$ tak, aby pro kořeny rovnice $9x^2 - 18px - 8p + 16 = 0$ platilo, že $x_1 = 2x_2$ .
(e) Určete, pro jaké $q\in\mathbb{R}$ je jeden kořen rovnice $x^2 -6x+q=0$ roven čtyřnásobku druhého.
(f) Pro které hodnoty parametru $a\in\mathbb R$ má rovnice $x^2-2ax+4a-1=0$ jeden kořen o dvě větší než druhý?
(g) Určete parametr $k\in\mathbb R$ rovnice $x^2+3x+k=0$ tak, aby pro kořeny rovnice platilo $|x_2-x_1|=2$ .
(h) Pro které hodnoty parametru $c\in\mathbb R$ splnují kořeny rovnice $x^2-2x+c=0$ vztah $7x_1-4x_2=47$ ?
(i) Určete všechny hodnoty parametru $a\in\mathbb R$ , pro které splňují kořeny rovnice

$x^2-3ax+a^2=0$

podmínku

$x_1^2+x_2^2=\frac{7}{4}$ .
(j) Pro které hodnoty parametru

$a\in\mathbb R$ splňují kořeny rovnice

$2x^2+6x+a=0$ podmínku

$\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}<2$ ?
(k) Pro které hodnoty parametru

$c\in\mathbb R$ je jeden kořen rovnice

$8x^2-6x+9c^2=0$ roven druhé mocnině druhého kořene?
(l) Pro které hodnoty parametru

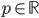$p\in\mathbb R$ je součet druhých mocnin kořenů rovnice

$x^2+px+35=0$ roven 74?
(m) Pro které hodnoty parametru

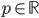$p\in\mathbb R$ je součet třetích mocnin kořenů rovnice

$x^2-x-p=0$ roven 19?
(n) Pro které hodnoty parametru

$a\in\mathbb R$ je součet kořenů rovnice

$x^2-2a(x-1)-1=0$ roven součtu druhých mocnin těchto kořenů?
(o) Pro které hodnoty parametru

$k\in\mathbb R$ jsou kořeny rovnice

$x^2-(2k+1)x+k^2=0$ v poměru 1:4?
(p) Pro které hodnoty parametru

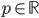$p\in\mathbb R$ je poměr kořenů rovnice

$x^2+px-16=0$ roven

$-4$ ?
(q) Určete parametr

$m\in\mathbb R$ tak, aby pro kořeny rovnice

$3x^2+mx-1=0$ platilo

$|x_1-x_1|=5$ .
(r) Určete parametr

$m\in\mathbb R$ tak, aby rovnice

$mx^2 + 8x + 4 = 0$ měla jeden kořen třikrát větší než druhý.
(s) Určete parametr

$q\in\mathbb R$ tak, aby kořeny rovnice

$2x^2-27x+q=0$ byly v poměru

$2:1$ .

Řešení	Ukázat
(a) Podle zadání a podle Vietových vztahů platí: $\begin{cases}x_1=2x_2\\ x_1x_2=2p+8\\ x_1+x_2=p\end{cases}\Rightarrow\begin{cases}2x_2^2=2p+8\\ 3x_2=p\end{cases}\Rightarrow p^2-9p-36=0$ $p=12\ \vee\ p=-3$ (b) $a=4$ (c) $k=-7\ \vee\ k=-1$ (d) $p=-2\ \vee\ p=1$ (e) $q=\frac{144}{25}$ (f) $a=0\ \vee\ a=4$ (g) $k=\frac54$ (h) $c=-15$ (i) $a=\pm\frac12$ (j) $a\in(0;\frac92)$ (k) $c=\pm\frac13$ (l) $p=\pm12$ (m) $p=6$ (n) $a=1$ (o) $k=2\ \vee\ k=-\frac29$ (p) $p=\pm6$ (q) $m=\pm\sqrt{213}$ (r) $m=3$ (s) $q=81$

Řešení

Ukázat

(a) Podle zadání a podle Vietových vztahů platí:

$\begin{cases}x_1=2x_2\\ x_1x_2=2p+8\\ x_1+x_2=p\end{cases}\Rightarrow\begin{cases}2x_2^2=2p+8\\ 3x_2=p\end{cases}\Rightarrow p^2-9p-36=0$

$p=12\ \vee\ p=-3$

(b) $a=4$ (c) $k=-7\ \vee\ k=-1$ (d) $p=-2\ \vee\ p=1$ (e) $q=\frac{144}{25}$ (f) $a=0\ \vee\ a=4$ (g) $k=\frac54$ (h) $c=-15$ (i) $a=\pm\frac12$ (j) $a\in(0;\frac92)$ (k) $c=\pm\frac13$ (l) $p=\pm12$ (m) $p=6$ (n) $a=1$ (o) $k=2\ \vee\ k=-\frac29$ (p) $p=\pm6$ (q) $m=\pm\sqrt{213}$ (r) $m=3$ (s) $q=81$

Příklad 9

(a) Určete počet řešení pro 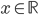$x\in\mathbb R$ rovnice $(a+5)x^2-(a+2)x+1=0$ v závislosti na parametru $a\in\mathbb R$ .
(b) Určete všechny hodnoty parametru $a\in\mathbb R$ tak, aby platilo $(a+1)x^2-3ax+4a\ne1$ .
(c) Určete všechny hodnoty parametru 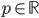$p\in\mathbb R$ , pro které má rovnice $px^2+(2p-1)x-2=0$ kořeny $x_1,x_2\in\langle-2;2\rangle$ .
(d) Pro které hodnoty parametru 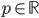$p\in\mathbb R$ splnují kořeny rovnice $x^2-2(p-3)x+p-1=0$ podmínky $x_1>1$ , $x_2>1$ ?
(e) Pro které hodnoty parametru $a\in\mathbb R$ mají rovnice $x^2+ax+1=0$ a $x^2+x+a=0$ jeden společný kořen?
(f) Pro které hodnoty parametru $a\in\mathbb R$ mají rovnice $x^2+ax+8=0$ a $x^2+x+a=0$ jeden společný kořen?
(g) Pro které hodnoty parametru 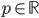$p\in\mathbb R$ mají rovnice $3x^2-4x+p-2=0$ a $x^2-2px+5=0$ jeden společný kořen? Určete tento kořen.
(h) Pro které hodnoty parametru $b\in\mathbb Z$ mají rovnice $2x^2+(3b-1)x-3=0$ a $6x^2-(2b-3)x-1=0$ jeden společný kořen?
(i) Rovnice $x^3+(a-1)x^2-ax+1=0$ a $x^2+ax+1=0$ mají právě jeden společný kořen. Určete hodnotu parametru $a\in\mathbb R$ .
(j) Dvě různé rovnice $(1):x^2+ax+b=0$ a $(2):x^2+cx+d=0$ ( $abcd\neq0$ ) mají právě jeden společný kořen. Vypočítejte druhý kořen rovnice $(2)$ .
(k) Pro které hodnoty parametru $a\in\mathbb R$ je součet druhých mocnin kořenů rovnice $x^2+ax+a-2=0$ nejmenší?
(l) Určete koeficienty kvadratické rovnice $x^2+px+q=0$ ( $p\ne q$ , $p,q\in\mathbb R$ ) tak, aby její kořeny byly rovny $p$ a $q$ .

Řešení	Ukázat
(a) $a\in(-\infty;-5)\cup(-5;-4)\cup(4;\infty)$ dvě řešení, $a\in\{\pm4;-5\}$ jedno řešení, $a\in(-4;4)$ žádné řešení (b) $a\in(-\infty;-2)\cup(\frac27;\infty)$ (c) $p\in(-\infty;-\frac12]\cup[\frac12;\infty)$ (d) $p\in(5;6)$ (e) $a=-2$ (f) $a=-6$ (g) $p=3$ $x=1$ nebo $p=-\frac{41}{12}$ $x=-\frac56$ (h) $b=2$ (i) $a=-\frac52$ (j) $x_2=\frac{d(a-c)}{d-b}$ (k) $a=1$ (l) $p=1$ $q=-2$

Příklad 10

(a) Za předpokladu, že $c\ne0$ a $x_1$ , $x_2$ jsou kořeny rovnice $3x^2+7x+c=0$ , vyjádřete $\dfrac{1}{x_1}+\dfrac{1}{x_2}$ .
(b) Když $x_1$ , $x_2$ jsou dvě různá řešení rovnice $2x^2-x-2=0$ , určete hodnotu výrazu $\dfrac{1}{x_1}+\dfrac{1}{x_2}$
(c) Čísla $r$ a $s$ jsou kořeny rovnice $x^2-6x+2=0$ . Vypočítejte $\displaystyle \frac{1}{r}+\frac{1}{s}$ .

Řešení	Ukázat
(a) $\frac{1}{x_1}+\frac{1}{x_2}=-\frac7c$ (b) $\frac{1}{x_1}+\frac{1}{x_2}=-\frac12$ (c) $\frac{1}{r}+\frac{1}{s}=3$

Příklad 11

(a) Napište kvadratickou rovnici jejíž jeden kořen je roven součtu a druhý součinu kořenů rovnice $ax^2+bx+c=0$ ( $a\ne0$ ).
(b) Napište kvadratickou rovnici jejíž kořeny jsou o 1 vetší než kořeny rovnice $ax^2+bx+c=0$ ( $a\ne0$ ). (c) Napište kvadratickou rovnici, jejíž kořeny jsou převrácená čísla ke kořenům rovnice $x^2-2x-2=0$ .
(d) Student při řešení kvadratické rovnice zaměnil koeficienty u kvadratického a absolutního členu. Novou rovnici vyřešil správně a dostal kořeny 1 a 2. Víme, že původní rovnice měla také jeden z kořenů 1. Napište původní rovnici.

Řešení	Ukázat
(a) $k[a^2x^2+a(b-c)x-bc]=0$ , $k\ne0$ (b) $k[ax^2-(2a-b)x+c-b+1]=0$ $k\ne0$ (c) $k(2x^2+2x-1)=0$ , $k\ne0$ (d) $k(2x^2-3x+1)=0$ $k\ne0$

Příklad 12

(a) Pro kolik reálných čísel $a$ má kvadratická rovnice $x^2+ax+2007=0$ dva celočíselné kořeny?
(b) Určete počet všech reálných čísel $b$ , pro než má rovnice $x^2-bx+80=0$ dva různé kořeny v množine sudých přirozených čísel.

Řešení	Ukázat
(a) Prvočíselný rozklad je $2007=3^2\cdot223$ . To znamená, že existuje šest hodnot pro $a$ ( $\pm2008$ , $\pm672$ a $\pm232$ ). (b) $80=2^4\cdot5$ . Jsou 3 možnosti: $a\in\{18;24;42\}$

Příklad 13

(a) Pro které hodnoty parametru $m\in\mathbb R$ má rovnice $4x^2-m=5|x|$ právě tři reálná řešení?
(b) Je dána rovnice $x^2-4=2|x|+k.$ Určete hodnotu parametru $k$ , když
(i) rovnice nemá žádné reálné řešení, (ii) rovnice má právě dvě reálná řešení.
(c) Určete všechny hodnoty parametru $a\in\mathbb R$ , pro které má rovnice $|x^2+2x+a|=2$ právě čtyři reálná řešení.

Řešení	Ukázat
(a) Z grafu je zřejmé, že pro $m=0$ . (b) Opět z grafu (i) $k\in(-\infty;-5)$ (ii) $k\in(-4;\infty)\cup\{-5\}$ (c) $a\in(-\infty;-1)$

Příklad 14

(a) Určete parametr $k\in\mathbb R$ tak, aby výraz $2x^3+kx^2+x$ byl dělitelný výrazem $x-1$ .
(b) Určete parametr $m\in\mathbb R$ tak, aby výraz $x^3-5x^2+7x+(m-5)$ byl dělitelný výrazem $x-4$ .
(c) Určete parametr $k\in\mathbb R$ tak, aby výraz $x^3+kx-3$ byl dělitelný výrazem $x-1$ .
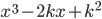(d) Pro které hodnoty parametru $k\in\mathbb R$ je výraz $x^3-2kx+k^2$ beze zbytku dělitelný výrazem $x+3$ ?

Řešení	Ukázat
(a) Nápověda: jeden kořen rovnice $2x^3+kx^2+x=0$ musí být roven jedné. $k=-3$ (b) $m=-7$ (c) $k=2$ (d) $k=3$

Příklad 15

Nechť $p$ , $q$ jsou prvočísla taková, že rovnice $px^2-qx+p=0$ má racionální kořeny. Určete součet $p+q$ .

Řešení	Ukázat
Řešení dané rovnice $x=\dfrac{q\pm\sqrt{q^2-4p^2}}{2p}$ bude racionální, když $q\ge2p$ a současně $q^2-4p^2$ bude kvadrát přirozeného čísla. Označme $q^2-4p^2=A^2\\ q^2=A^2+4p^2,$ $A\in\mathbb N$ . Poslední vztah je rovnice pro Pythagorejské trojice, která má řešení $q=u^2+v^2$ a $2p=u^2-v^2\ \vee\ 2p=2uv$ , $u>v$ , $u,v\in\mathbb N$ . První možnost $2p=u^2-v^2\\2p=(u+v)(u-v)\\ \begin{cases}2=u+v\\ p=u-v\end{cases}\ \vee\ \begin{cases}2=u-v\\ p=u+v\end{cases}\ \vee\ \begin{cases}2p=u+v\\1=u-v\end{cases}$ nemá v přirozených číslech řešení. Druhá možnost $2p=2uv\\ p=uv\\ u=p\ \wedge\ v=1\\q=p^2+1$ Protože $q$ je liché prvočíslo, musí být $p$ sudé prvočíslo. Je tedy $p=2$ , $q=5$ a $p+q=7$ .

Řešení

Ukázat

Řešení dané rovnice

$x=\dfrac{q\pm\sqrt{q^2-4p^2}}{2p}$

bude racionální, když

$q\ge2p$ a současně

$q^2-4p^2$ bude kvadrát přirozeného čísla. Označme

$q^2-4p^2=A^2\\ q^2=A^2+4p^2,$

$A\in\mathbb N$ . Poslední vztah je rovnice pro Pythagorejské trojice, která má řešení

$q=u^2+v^2$ a

$2p=u^2-v^2\ \vee\ 2p=2uv$ ,

$u>v$ ,

$u,v\in\mathbb N$ .

První možnost

$2p=u^2-v^2\\2p=(u+v)(u-v)\\ \begin{cases}2=u+v\\ p=u-v\end{cases}\ \vee\ \begin{cases}2=u-v\\ p=u+v\end{cases}\ \vee\ \begin{cases}2p=u+v\\1=u-v\end{cases}$

nemá v přirozených číslech řešení.

Druhá možnost

$2p=2uv\\ p=uv\\ u=p\ \wedge\ v=1\\q=p^2+1$

Protože

$q$ je liché prvočíslo, musí být

$p$ sudé prvočíslo. Je tedy

$p=2$ ,

$q=5$ a

$p+q=7$ .

rovnice

Velká kniha rovnic

Kvadratické rovnice s parametrem

Příklad 1

Příklad 2

Příklad 3

Příklad 4

Příklad 5

Příklad 6

Příklad 7

Příklad 8

Příklad 9

Příklad 10

Příklad 11

Příklad 12

Příklad 13

Příklad 14

Příklad 15