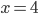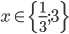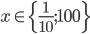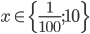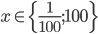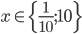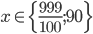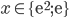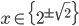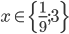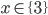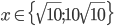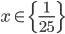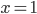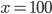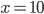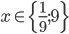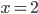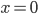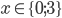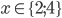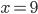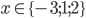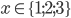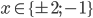Příklad 1
Řešte rovnice pro 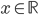 :
:
(a) 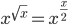
|
(b) 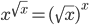
|
| Řešení | Ukázat |
|---|---|
Příklad 2
Řešte rovnice pro 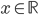 :
:
(a) 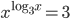
|
(b) 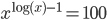
|
(c) 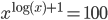
|
(d) 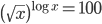
|
(e) 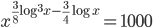
|
(f) 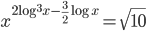
|
(g) 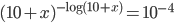
|
(h) 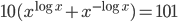
|
| Řešení | Ukázat |
|---|---|
Příklad 3
Řešte rovnice pro 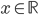 :
:
(a 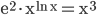
|
(b) 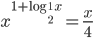
|
(c) 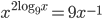
|
(d) 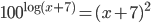
|
(e) 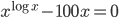
|
(f) 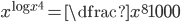
|
(g) 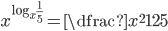
|
(h) 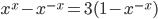
|
| Řešení | Ukázat |
|---|---|
Příklad 4
Řešte rovnice pro 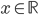 :
:
(a) 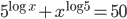
|
(b) 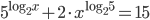
|
(c) 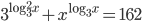
|
(d) 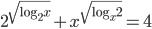
|
| Řešení | Ukázat |
|---|---|
Příklad 5
Řešte rovnice pro 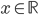 :
:
(a) 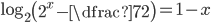
|
(b) 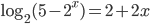
|
(c) 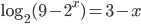
|
(d) 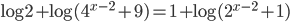
|
(e) 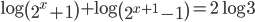
|
(f) 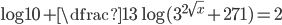
|
| Řešení | Ukázat |
|---|---|
Příklad 6
Řešte rovnice pro 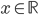 :
:
(a) 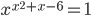
|
(b) 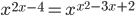
|
(c) 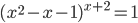
|
| Řešení | Ukázat |
|---|---|