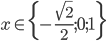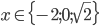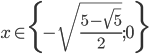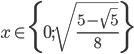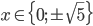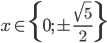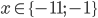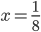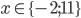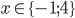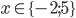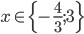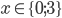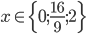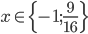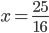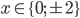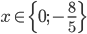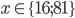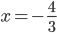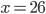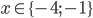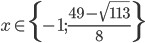Příklad 1
V množině reálných čísel řešte rovnice
(a) 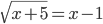
|
(b) 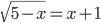
|
(c) 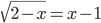
|
(d) 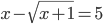
|
(e) 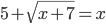
|
(f) 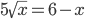
|
(g) 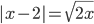
|
(h) 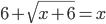
|
(i) 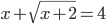
|
(j) 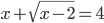
|
(k) 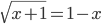
|
(l) 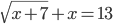
|
(m) 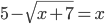
|
(n) 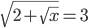
|
| Řešení | Ukázat |
|---|---|
Příklad 2
V množině reálných čísel řešte rovnice
(a) 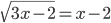
|
(b) 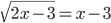
|
(c) 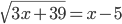
|
(d) 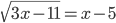
|
(e) 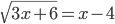
|
(f) 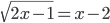
|
(g) 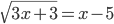
|
(h) 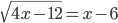
|
(i) 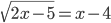
|
(j) 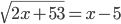
|
(k) 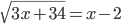
|
(l) 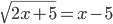
|
(m) 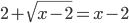
|
(n) 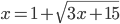
|
(o) 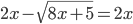
|
(p) 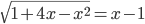
|
| Řešení | Ukázat |
|---|---|
Příklad 3
V množině reálných čísel řešte rovnice
(a) 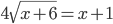
|
(b) 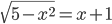
|
(c) 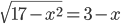
|
(d) 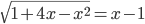
|
(e) 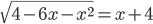
|
(f) 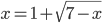
|
(g) 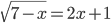
|
(h) 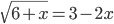
|
(i) 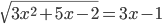
|
(j) 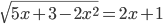
|
(k) 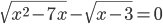
|
(l) 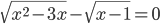
|
(m) 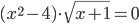
|
(n) 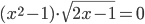
|
(o) 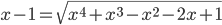
|
(p) 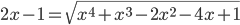
|
| Řešení | Ukázat |
|---|---|
Příklad 4
V množině reálných čísel řešte rovnice
(a) 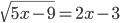
|
(b) 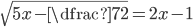
|
(c) 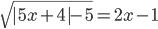
|
(d) 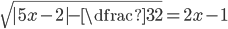
|
(e) 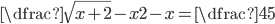
|
(f) 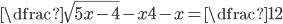
|
(g) 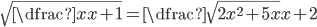
|
(h) 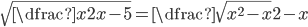
|
(i) 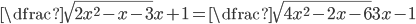
|
(j) 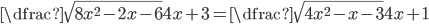
|
(k) ![\sqrt[3]{\dfrac{3x+1}{x-1}}=\sqrt{\dfrac{3x+1}{x+1}}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_917491d9bb29f64d3abc0d8e2ac8d49c.gif)
|
(l) ![\sqrt[3]{\dfrac{2x-1}{x+1}}=\sqrt{\dfrac{2x-1}{x-1}}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_803972788a0fc43c99ea9b7f918387fa.gif)
|
| Řešení | Ukázat |
|---|---|
Příklad 5
V množině reálných čísel řešte rovnice
(a) 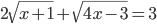
|
(b) 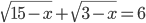
|
(c) 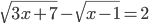
|
(d) 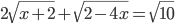
|
(e) 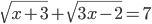
|
(f) 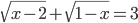
|
(g) 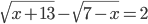
|
(h) 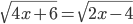
|
(i) 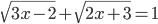
|
(j) 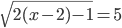
|
(k) 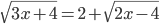
|
(l) 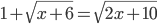
|
(m) 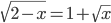
|
(n) 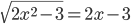
|
(o) 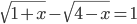
|
(p) 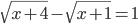
|
(q) 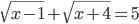
|
(r) 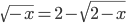
|
(s) 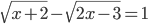
|
(t) 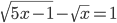
|
(u) 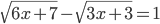
|
(v) 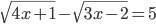
|
(w) 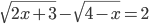
|
(x) 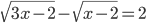
|
(y) 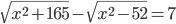
|
(z) 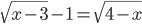
|
| Řešení | Ukázat |
|---|---|
Příklad 6
V množině reálných čísel řešte rovnice
(a) 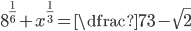
|
(b) 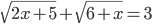
|
(c) 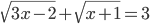
|
(d) 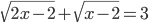
|
(e) 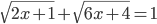
|
(f) 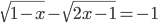
|
(g) 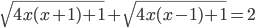
|
(h) 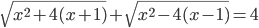
|
(i) 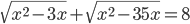
|
(j) 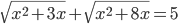
|
(k) 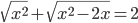
|
(l) 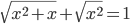
|
(m) 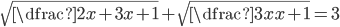
|
(n) 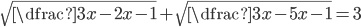
|
(o) 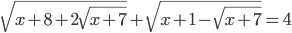
|
(p) 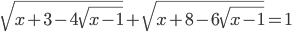
|
| Řešení | Ukázat |
|---|---|
Příklad 7
V množině reálných čísel řešte rovnice
(a) 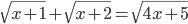
|
(b) 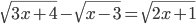
|
(c) 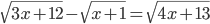
|
(d) 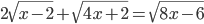
|
(e) 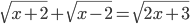
|
(f) 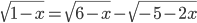
|
(g) 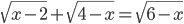
|
(h) 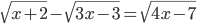
|
(i) 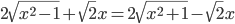
|
(j) 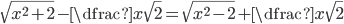
|
(k) 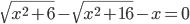
|
(l) 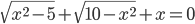
|
(m) 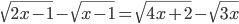
|
(n) 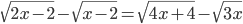
|
| Řešení | Ukázat |
|---|---|
Příklad 8
V množině reálných čísel řešte rovnice
(a) ![x\cdot\sqrt{x^2+15}-\sqrt x\cdot\sqrt[4]{x^2+15}=2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2f8866f19de7a3a633c2d2192d1be699.gif)
|
(b) 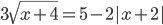
|
(c) 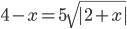
|
(d) 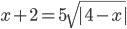
|
(e) 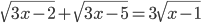
|
(f) 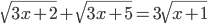
|
(g) 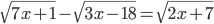
|
(h) 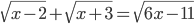
|
(i) 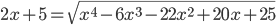
|
(j) 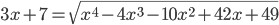
|
(k) 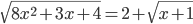
|
(l) 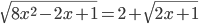
|
(m) 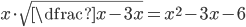
|
(n) 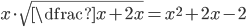
|
(o) 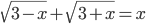
|
(p) 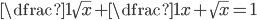
|
(q) 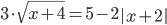
|
| Řešení | Ukázat |
|---|---|
Příklad 9
V množině reálných čísel řešte rovnice
(a) 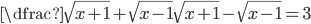
|
(b) 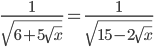
|
(c) 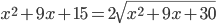
|
(d) 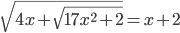
|
(e) 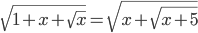
|
(f) 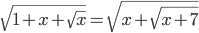
|
(g) 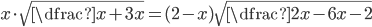
|
(h) 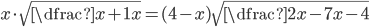
|
(i) 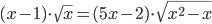
|
(j) 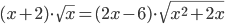
|
| Řešení | Ukázat |
|---|---|
Příklad 10
V množině reálných čísel řešte rovnice
(a) 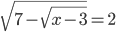
|
(b) 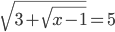
|
(c) 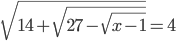
|
(d) 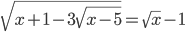
|
(e) 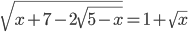
|
(f) 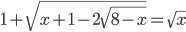
|
(g) 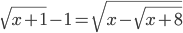
|
(h) 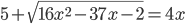
|
(i) 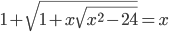
|
(j) 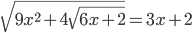
|
(k) 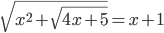
|
(l) 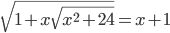
|
(m) 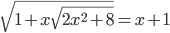
|
(n) 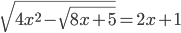
|
(o) 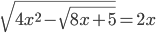
|
(p) 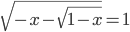
|
| Řešení | Ukázat |
|---|---|
Příklad 11
V množině reálných čísel řešte rovnice
(a 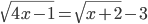
|
(b) 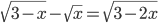
|
(c) 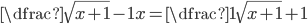
|
(d) 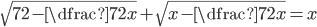
|
(e) 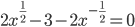
|
(f) 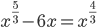
|
(g) 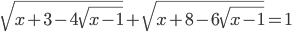
|
(h) 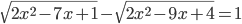
|
(i) 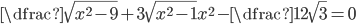
|
(j) 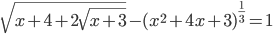
|
(k) 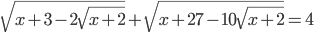
|
(l) 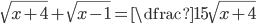
|
(m) ![\sqrt[3]{x^3+3x^2-4x+1}=\dfrac12+\left|x-\dfrac12\right|](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_41463ebcc06b9449d7d2168168a7e839.gif)
|
(n) ![\sqrt[3]{8+16x+6x^2-x^3}=|x+1|+1](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3a381edb5dece3926baec7c3d796c3ce.gif)
|
(o) 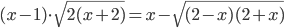
|
(p) 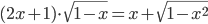
|
(q) ![\sqrt[3]{x+2}+\sqrt[3]{x-2}=x](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ac6b6dc59ab5d418bee40c2d3c656f94.gif)
|
(r) ![\sqrt[3]{\dfrac{(x+1)^2}2}-\sqrt[3]{\dfrac{(x-1)^2}2}=x](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_603e64ba129cd3e2d2f78dc6edfd6c71.gif)
|
| Řešení | Ukázat |
|---|---|
Příklad 12
Vhodnou substitucí řešte v množině reálných čísel rovnice
(a) 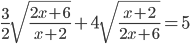
|
(b) 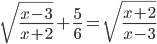
|
(c) 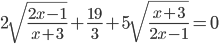
|
(d) 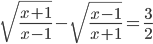
|
(e) 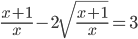
|
(f) ![\displaystyle \sqrt[3]{\frac{25-x}{3+x}}+3\sqrt[3]{\frac{3+x}{25-x}}=4](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f0a24948ed12673b8050bd59ea15ae36.gif)
|
(g) 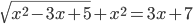
|
(h) 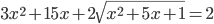
|
(i) 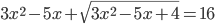
|
(j) 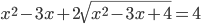
|
(k) 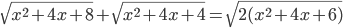
|
| Řešení | Ukázat |
|---|---|
Příklad 13
V množině reálných čísel řešte rovnice
(a) ![\sqrt[4]{x+8}-\sqrt[4]{x-8}=2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_27f3b4d7bf468e82e91588935c02b6df.gif)
|
(b) ![x\sqrt {x^{2}+15}-\sqrt {x}\cdot \sqrt[4]{x^{2}+15}=2](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2919277ac24411a960a3803a14ac98c0.gif)
|
(c) 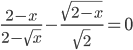
|
(d) 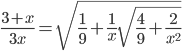
|
(e) 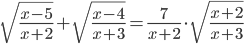
|
(f) 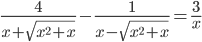
|
(g) 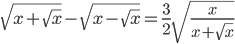
|
(h) 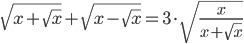
|
(i) 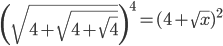
|
(j) ![\displaystyle \sqrt{\sqrt{x^2+2}+x}-\sqrt{\sqrt{x^2+2}-x}=2\cdot\sqrt[4]{2}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f75b078a0fe58d73e2d7676307a24783.gif)
|
(k) 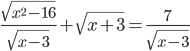
|
(l) 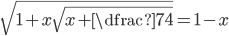
|
(m) 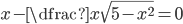
|
(n) 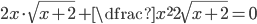
|
| Řešení | Ukázat |
|---|---|
Příklad 14
V množině reálných čísel řešte rovnici
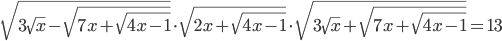
| Řešení | Ukázat |
|---|---|
Příklad 15
V množině reálných čísel řešte rovnice
(a) 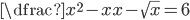
|
(b) 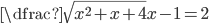
|
| Řešení | Ukázat |
|---|---|
Příklad 16
V množině reálných čísel řešte rovnice
(a) 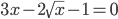
|
(b) ![\sqrt x-5\cdot\sqrt[4]{x}+6=0](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f0d6ab711d00165fc174849bda0148df.gif)
|
(c) 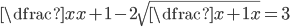
|
(d) 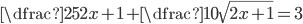
|
(e) 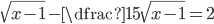
|
(f) 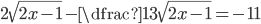
|
(g) 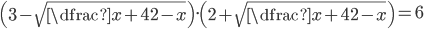
|
(h) 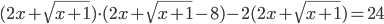
|
| Řešení | Ukázat |
|---|---|
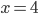
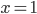
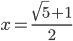
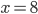
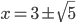
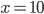
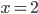
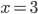
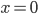
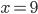

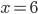

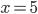
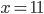

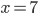
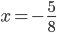
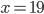
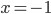
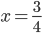
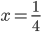
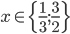
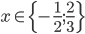
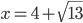
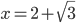
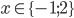
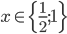
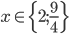
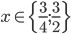
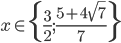
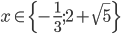
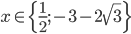
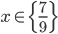
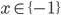
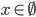
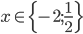
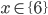
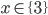
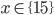
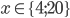
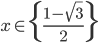
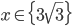
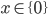
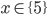
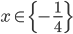

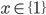
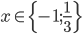
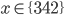
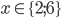
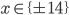
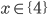
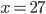
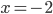
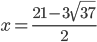
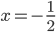
![x\in[-\frac12;\frac12]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a21e14913d792f7e07f31d14a3b1ffe3.gif)
![x\in[-2;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_477fb206c0a1c268595ce4cd958039ea.gif)
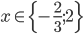
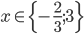
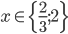
![x\in[5;10]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a1cc415af89db86a9096a553d780827b.gif)
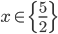
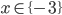
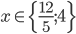
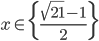
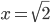
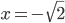
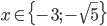
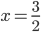
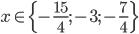
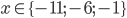
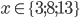
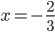
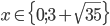
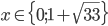
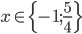
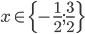
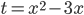
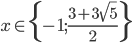
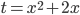
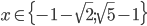
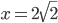
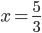
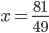
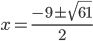
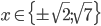
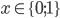
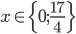
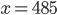
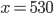
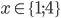
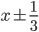
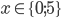
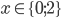
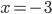
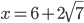
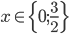
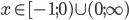
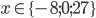
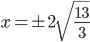
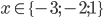
![x\in[-1;23]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_33d69a6acc91493a069325640cd1eb09.gif)