Příklad 1
V množině 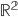 řešte soustavy
řešte soustavy
(a) 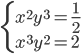
|
(b) 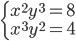
|
(c) 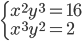
|
(d) 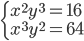
|
(e) 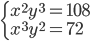
|
(f) 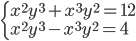
|
| Řešení | Ukázat |
|---|---|
Příklad 2
V množině 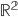 řešte soustavy
řešte soustavy
(a) 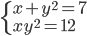
|
(b) 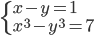
|
(c) 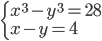
|
(d) 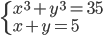
|
(e) 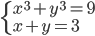
|
(f) 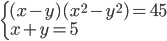
|
(g) 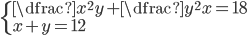
|
(h) 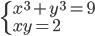
|
| Řešení | Ukázat |
|---|---|
Příklad 3
V množině 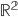 řešte soustavy
řešte soustavy
(a) 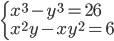
|
(b) 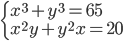
|
(c) 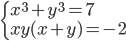
|
(d) 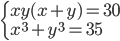
|
(e) 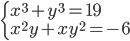
|
(f) 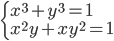
|
(g) 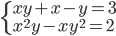
|
(h) 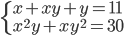
|
(i) 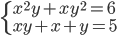
|
(j) 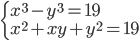
|
(k) 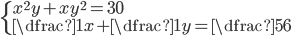
|
(l) 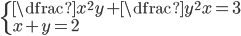
|
| Řešení | Ukázat |
|---|---|
Příklad 4
V množině 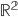 řešte soustavy
řešte soustavy
(a) 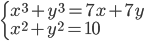
|
(b) 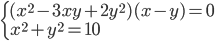
|
(c) 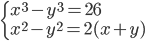
|
(d) 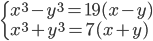
|
(e) 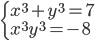
|
(f) 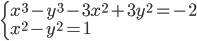
|
(g) 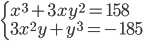
|
(h) 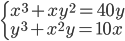
|
(i) 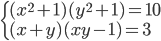
|
(j) 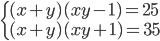
|
(k) 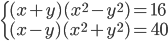
|
(l) 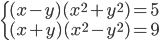
|
| Řešení | Ukázat |
|---|---|
Příklad 5
V množině 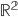 řešte soustavy
řešte soustavy
(a) 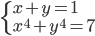
|
(b) 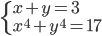
|
(c) 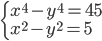
|
(d) 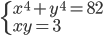
|
(e) 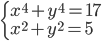
|
(f) 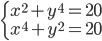
|
(g) 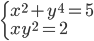
|
(h) 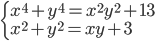
|
(i) 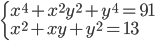
|
(j) 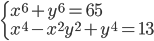
|
(k) 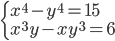
|
(l) 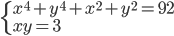
|
(m) 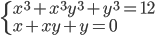
|
(n) 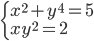
|
| Řešení | Ukázat |
|---|---|
Příklad 6
V množině 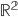 řešte soustavy
řešte soustavy
(a) ![\begin{cases} \sqrt[3]{x}+\sqrt[3]{y}=3\\xy=8 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fbf3cb4abceeac612a3f553511fd3a55.gif)
|
(b) ![\begin{cases} \sqrt[3]{x}+\sqrt[3]{y}=4\\xy=27 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_86d6bd8f36dc4e4aaf76a295efab0075.gif)
|
(c) ![\begin{cases} \sqrt[3]{x}+\sqrt[3]{y}=4\\x+y=28 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_02d71e91109f24d0364502eb06d26e3b.gif)
|
(d) 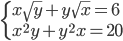
|
(e) 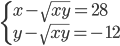
|
(f) 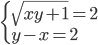
|
(g) 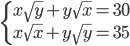
|
(h) 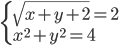
|
(i) 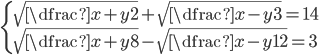
|
(j) 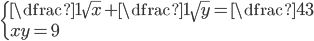
|
(k) 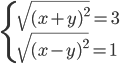
|
(l) ![\begin{cases}\sqrt x+\sqrt y=10\\\sqrt[4]x+\sqrt[4]y=4 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0f5f2f39327c1bf445fe5eed1534afda.gif)
|
(m) ![\begin{cases}\sqrt[4]x-\sqrt[4]y=1\\ \sqrt x+\sqrt y=5 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6bc03c09e89863224c0e7807694bc690.gif)
|
(n) ![\begin{cases}\sqrt[4]{x+y}+\sqrt[4]{x-y}=4\\ \sqrt{x+y}-\sqrt{x-y}=8 \end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e6c4df76d5d6d9d1030b8890402913dc.gif)
|
(o) ![\begin{cases}\sqrt[3]{\dfrac{x+y}{x-y}}-\sqrt[3]{\dfrac{x-y}{x+y}}=\dfrac32\\ x^2-y^2=32\end{cases}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7ad63615611df5613243e45a786e10a9.gif)
|
(p) 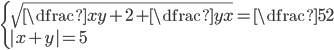
|
(q) 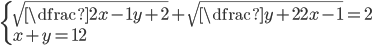
|
(r) 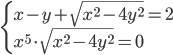
|
| Řešení | Ukázat |
|---|---|
Příklad 7
V množině 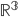 řešte soustavy
řešte soustavy
(a) 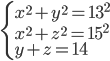
|
(b) 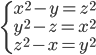
|
(c) 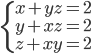
|
| Řešení | Ukázat |
|---|---|
![[x;y]=[2;\frac12]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6676cc5de8a13e19aa786278ec16d6d1.gif)
![[x;y]=[1;2]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ff95e09bf7e89bf3f594adfb85e884be.gif)
![[x;y]=[\frac12;4]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6ff53d4d5f7ae1cb4e147e693c223a5c.gif)
![[x;y]=[4;1]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cc2a973f99c69e418cbd38cbb1b02662.gif)
![[x;y]=[2;3]](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_cbd59427bbd1e5640e6fe86522b9e529.gif)
![[x;y]\in\{[3;\pm2];[4\pm\sqrt3;]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a9ca60cec4fbffad7d80897eb72a72f1.gif)
![[x;y]\in\{[-1;2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_78d7ccfe368de68ba9af8e084c7c010e.gif)
![[x;y]\in\{[1;-3];[3;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_188bcfacd732a74d4c231320a0aba004.gif)
![[x;y]\in\{[2;3];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fb84be51535e320568e2c2b0fe4fad0f.gif)
![[x;y]\in\{[1;2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_feed30da8085687c6a4c862da1f7ba2d.gif)
![[x;y]\in\{[1;4];[4;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f65701301534713d4b7ec9c145f9c221.gif)
![[x;y]\in\{[4;8];[8;4]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1b48432aaa7246e657be830dd716c997.gif)
![[x;y]\in\{[-1;-3];[3;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_908351fda05ce51055e64d30e9419058.gif)
![[x;y]\in\{[-1;2];[2;-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b28fbe5e7f8e59c0c6c2d33b4547e13b.gif)
![[x;y]\in\{[-2;3];[3;-2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_9a718cec6691d465efb3572c0a764d5a.gif)
![[x;y]\in\{[\frac1{\sqrt[3]2};\frac1{\sqrt[3]2}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ba67cbf9bccd2890c97329248fb136c1.gif)
![[x;y]\in\{[-1;-2];[2;1];[1\pm\sqrt2;-1\pm\sqrt2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_643904d47fcdfe7b184d12b46391bfec.gif)
![[x;y]\in\{[1;5];[2;3];[3;2];[5;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_61ce6f2da6f0a1c7c81782c60cd69b1a.gif)
![[x;y]\in\{[-2;-3];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f03639ee62ad84d7e1c8a4783b2349ec.gif)
![[x;y]\in\{[-6;1];[1;-6];[2;3];[3;2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f0bb6bb2b9906602b3ac148c6adc9205.gif)
![[x;y]\in\{[\frac23;\frac43];[\frac43;\frac23]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_8ce1bf3ee8ca64cde0bab0d427c57799.gif)
![[x;y]\in\{[\pm3;\pm1];[\pm1;\pm3];[\pm\sqrt5;\mp\sqrt5\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_698666870ce68a6c3fb131d8e1290b96.gif)
![[x;y]\in\{[\pm2\sqrt2;\pm\sqrt2];\pm\sqrt5;\pm\sqrt5\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_0b39267aff90902b82bfe41ae16071dd.gif)
![[x;y]\in\{[-1;-3];[3;1];[\sqrt[3]{13};-\sqrt[3]{13}\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_21f1fb0c2105265dfd587ecde0185b9f.gif)
![[x;y]\in\{[\pm3;\pm2];[0;0];[\pm2;\pm3];[\pm\sqrt7;\pm\sqrt7];[\pm\sqrt{19};\mp\sqrt{19}]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_a05bbce1b64ecd3037de4c4bbe783aa7.gif)
![[x;y]\in\{[1;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_79124fb99252920e535eb573c300d34a.gif)
![[x;y]\in\{[2;-5]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_fdecbf0745ab00f794db2c6b4181f8d6.gif)
![[x;y]\in\{[\pm4;\pm2];[0;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_448a146d165bd84182607f0553465fec.gif)
![[x;y]\in\{[-3;0];[\pm2;1];[1;\pm2];[0;-3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_931174192d21a90a7617181968a07541.gif)
![[x;y]\in\{[-1;-2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7942e8a693ad798706f7a3c13e2da42d.gif)
![[x;y]\in\{[\frac{1\pm\sqrt5}2;\frac{1\mp\sqrt5}2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_68152ca4f144a771bfafb1562cbfabc8.gif)
![[x;y]\in\{[-\sqrt7;\pm\sqrt2];[\sqrt7;\pm\sqrt2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7b5f50fb9eb3d8fce1f6e090fcde152d.gif)
![[x;y]\in\{[\pm3;\pm1];[\pm1;\pm3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e5ef0c97d5eaf82a3d471a8fd2baf08c.gif)
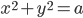
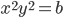
![[x;y]\in\{[-2;\pm1];[-1;\pm2];[1;\pm2];[2;\pm-1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7c90c1d15f46449277451192d961609a.gif)
![[x;y]\in\{[-2;\pm2];[2;\pm2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ce06e856eab801b5b6c9e13d8427ca7e.gif)
![[x;y]\in\{[1;\pm\sqrt2];[2;\pm1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ab38502c916952a6e0bbcda1ca3f9bca.gif)
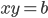
![[x;y]\in\{[\pm2;\pm1];[\pm1;\pm2];[\pm\sqrt{2-\sqrt3};\pm\sqrt{2-\sqrt3}(2+\sqrt3)];[\pm\sqrt{2+\sqrt3};\mp\sqrt{2+\sqrt3}(\sqrt3-2)]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_72da345d8205ef86c658570e1716a843.gif)
![[x;y]\in\{[-2;\pm1];[-1;\pm2];[1;\pm2];[2;\pm1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_071102bb191bc58a4a2da8c3dd0e1b4f.gif)
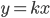
![[x;y]\in\{[-2;-1];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b31cc5555aa4a799ed3b7c7db70c4a9d.gif)
![[x;y]\in\{[\pm3;\pm1];[\pm1;\pm3\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_773303dd991d3430f6d5edf40cd2e4ce.gif)
![[x;y]\in\{[1-\sqrt3;1+\sqrt3];[1+\sqrt3;1-\sqrt3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ceeaf3149c2e157223d347f57398e850.gif)
![[x;y]\in\{[1;8];[8;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_bb4cd3f7b2c0fb4f2ff205da9706bb4d.gif)
![[x;y]\in\{[1;27];[27;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_275c89db4314c89c558fc94e7104011b.gif)
![[x;y]\in\{[49;9]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_b5d0de9aa9c162e579b30650b9d67932.gif)
![[x;y]\in\{[-3;-1];[1;3]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_f222e9b26f50168684554cee810dc690.gif)
![[x;y]\in\{[4;9];[9;4]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_d061de9b9674a2621e0d621690f64c7d.gif)
![[x;y]\in\{[0;2];[2;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6520bd247d3fcd6bb09d0115aec2d6b3.gif)
![[x;y]\in\{[124;76]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_1ec3bed4a1300f51013b4effd811e673.gif)
![[x;y]\in\{[1;9];[9;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_7921f178142084096f3de381cccd3665.gif)
![[x;y]\in\{[-2;-1];[-1;-2];[1;2];[2;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_e0f850346780bfebfe9534005084ece0.gif)
![[x;y]\in\{[1;81];[81;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_39855202d77219bc0c4534cc4c9812a6.gif)
![[x;y]\in\{[16;1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_2085b376018da331325cb2eafbeb956f.gif)
![[x;y]\in\{[41;40]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_9a088a1e266afe44ba74a08f2c127b63.gif)
![[x;y]\in\{[-9;-7];[9;7]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_beb736a445b47a7c639dbaf0f84db72d.gif)
![[x;y]\in\{[\pm1;\pm4];[\pm4;\pm1]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_ebdb44a321186e6e345f43212a367c3d.gif)
![[x;y]\in\{[5;7]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_3edbf393798643ea8176faa9274e62f3.gif)
![[x;y]\in\{[4;2];[\frac43;-\frac23]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_101aec63b4237135932d46104d384138.gif)
![[x;y;z]\in\{[\pm12;5;9]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_6cecaede40f23981e1d78383294744df.gif)
![[x;y;z]\in\{[0;0;0];[0;-1;1];[1;0;-1];[-1;1;0]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_883b37a42091dc229c813174b79c8630.gif)
![[x;y;z]\in\{[1;1;1];[-2;-2;-2]\}](http://vkr.rubesz.cz/wp-content/plugins/latex/cache/tex_475a599fa563995f38ff933dc59d59f0.gif)